CUDA 编程使用 Tensor core 详解

前言

最近在学习怎么使用 Tensor core.
主要通过 NVIDIA 官方文档和
cuda-samples 项目中关于 Tensor core 部分的实际代码示例结合其他文章做出总结,
再结合使用过程中的一些问题写出这篇文章.
本文首先解释了什么是 Tensor core 再详细说明在实际编程中如何使用 Tensor core.

文章链接 : CUDA 编程使用 Tensor core 详解

什么是 Tensor core

在 2017 GPU 技术大会(GTC 2017)上, NVIDIA推出了新一代 Volta 架构,
以及使用新架构的第一款设备 : 适用于深度学习任务的加速卡 Tesla V100.
Tesla V100 GPU架构首次搭搭载了张量核心(Tensor core).
Volta 架构中每一个 SM 中在固有的 CUDA core 基础上额外搭载了8个 Tensor core.
Tensor core 主要设计用于加速矩阵计算.

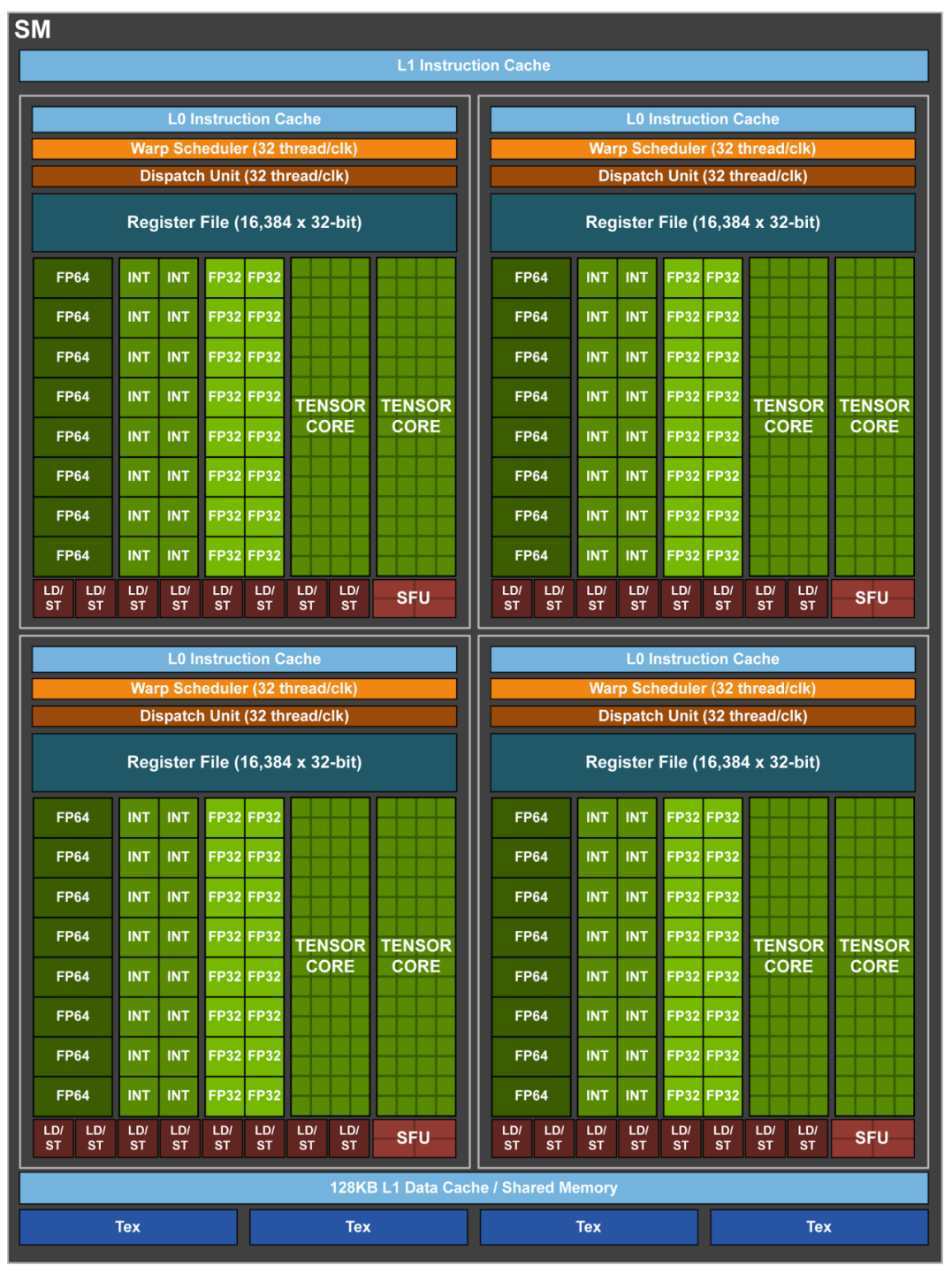
Tesla V100单个SM架构图

Tensor Core 是执行矩阵乘法累加的运算单元, 并且是混合精度的计算.
将两个半精度(FP16)矩阵相乘, 并将结果累积到一个累加矩阵中.

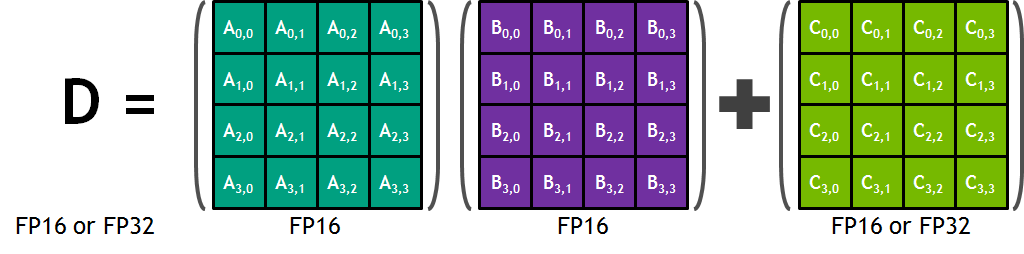
Tensor Core 执行4x4x4矩阵相乘累加

每个 Tensor Core 每时钟周期能执行 4x4x4 个矩阵运算, 执行运算 D = A * B + C, 其中 A, B, C, D 是 4×4 矩阵.
A, B是半精度(FP16)的矩阵, 累加矩阵C, D可以是半精度(FP16)或单精度(FP32)的矩阵.

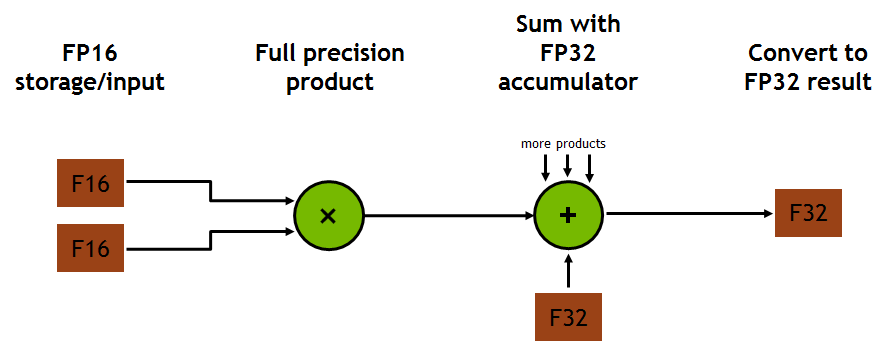
混合精度计算是指在底层硬件算子层面, 使用半精度(FP16)作为输入和输出, 使用全精度(FP32)进行中间结果计算和保存从而不损失过多精度的技术.

Tensor core 中的混合精度相乘和累积操作

为什么使用 Tensor core

Tesla V100 单个 SM 架构图中可以看到, 单个 SM 中分为4个 sub core.
一个 sub core 中的 CUDA core 单个时钟周期可以执行 16 次 FFMA 操作.
**一个 sub core 中有两个 Tensor core, 单个 Tensor core 每个时钟可以执行 64 次 FFMA 混合精度运算(FP16 乘法与 FP32
累加). **
比起 CUDA core, 使用 Tensor core 的吞吐量提升了8倍.

FFMA(Fused Floating-Point Multiply-Add)是一种在 GPU 上执行的高效数学运算,
将 32 位浮点数的乘法和加法两个操作融合在一个指令中完成, 从而提高性能和减少计算延迟.

Tesla V100 在一个 SM 单元中有8个 TensorCore, 每个时钟可执行共计 1024 次浮点运算.
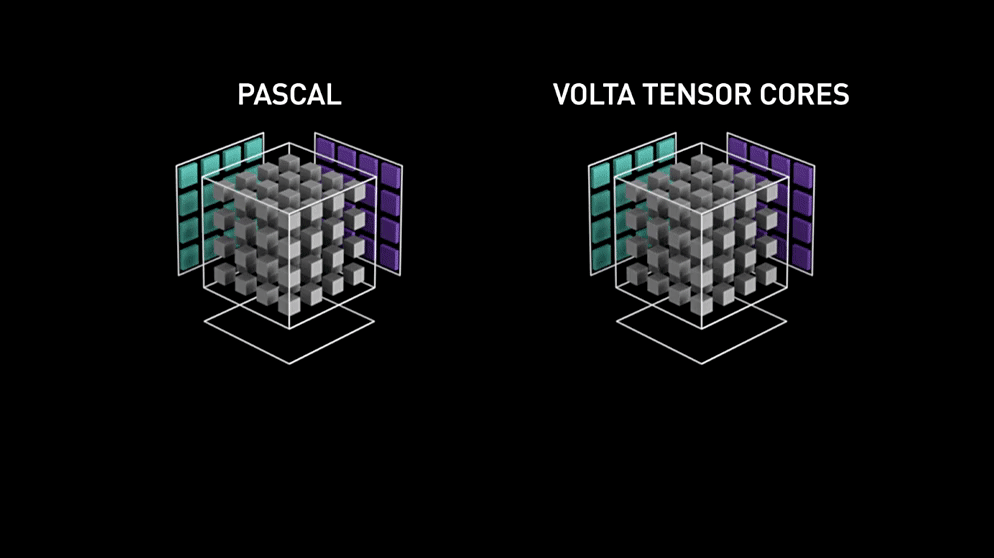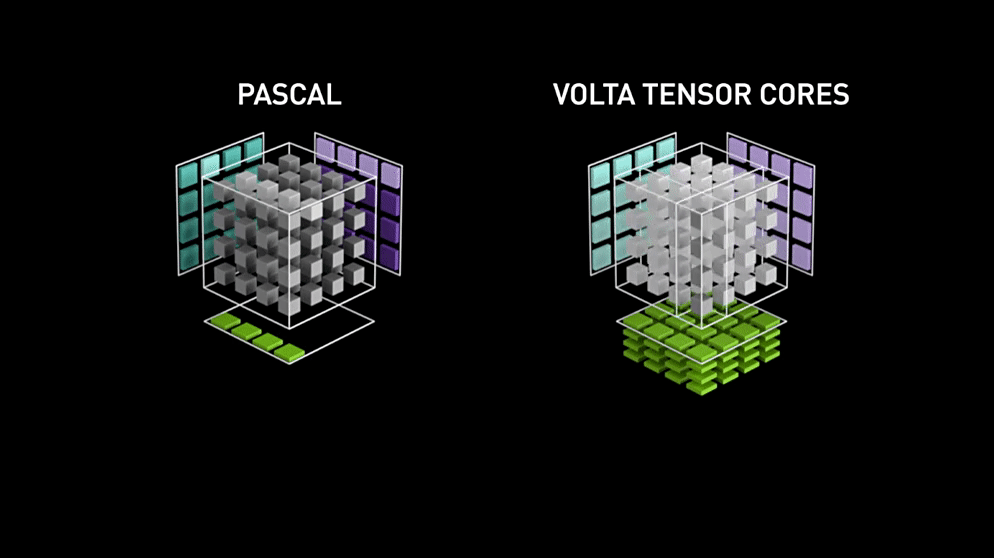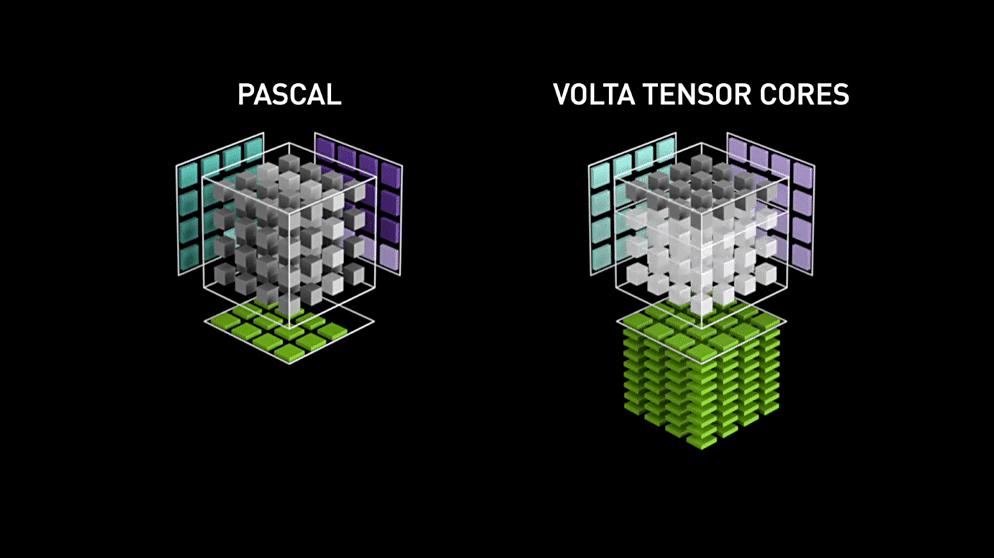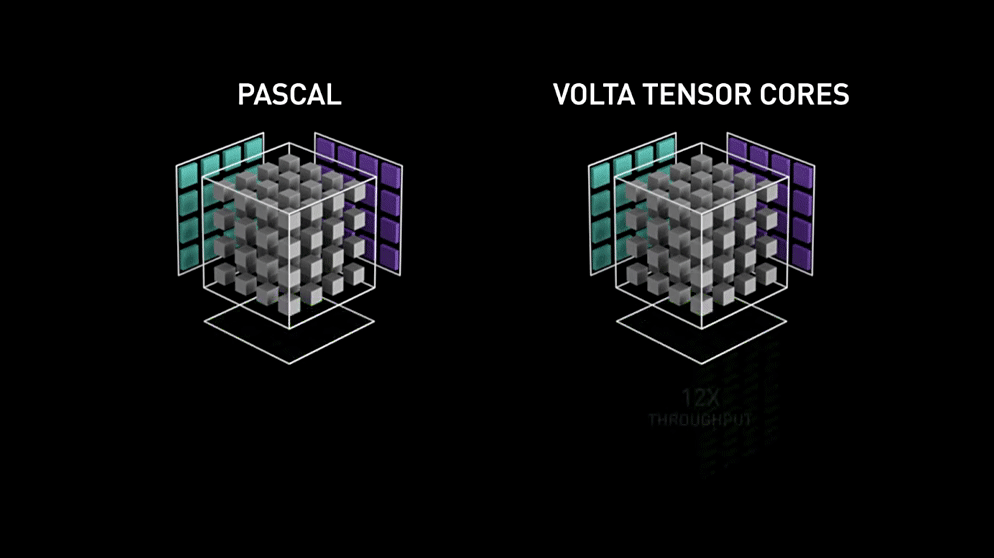
使用 Volta 架构的 V100 GPU 相比于上一代 Pascal 架构的 P100 GPU 的吞吐量一共提升了 12 倍.

Pascal架构和Volta架构矩阵运算速度对比

CUDA core 中, 每次进行一个点和一行进行相乘依次得到新的矩阵, 而 Tensor core 中是一个矩阵和另一个矩阵直接相乘得到新的矩阵.

运算从依次从一行和一列进行相乘得到结果,变化到一个矩阵与另一个矩阵直接相乘得到结果, 则编程思路也要进行变化.
下一节说明使用 Tensor core 的思路.

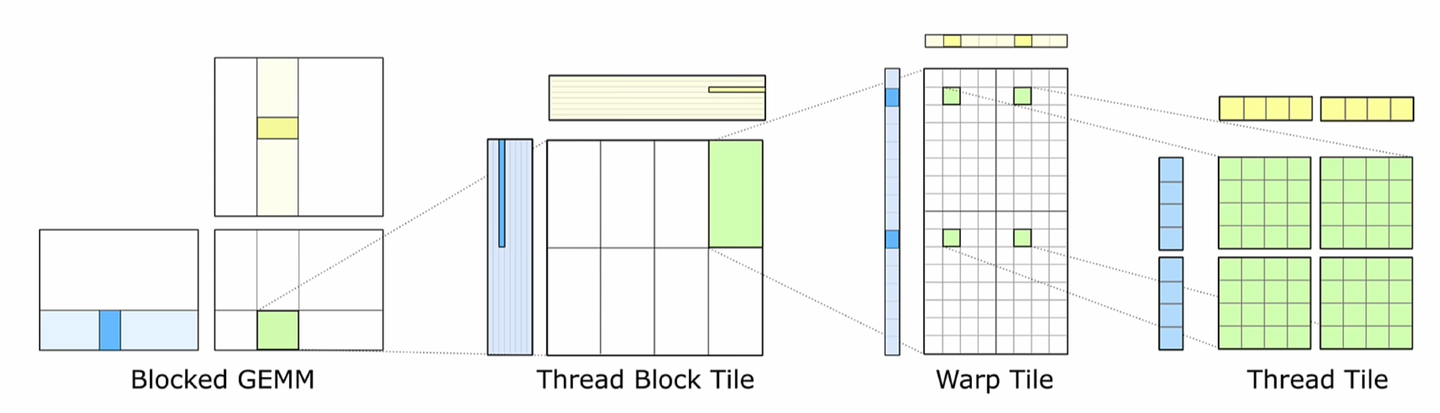
分块(tilling)

矩阵乘法一般使用分块 (tilling) 技术将大矩阵划分为许多小块 (tile) 分别进行计算,
通过对小块矩阵进行乘法运算, 降低了算法的时间复杂度, 并能够更好地利用缓存.
而每一个结果矩阵的块 (tile) 都是由
两个相乘矩阵 (A, B矩阵) 的块 (tile) 沿着 K 维度 (A矩阵的行, B矩阵的列) 相乘并累加得到的.

计算和储存匹配CUDA模型的分层结构

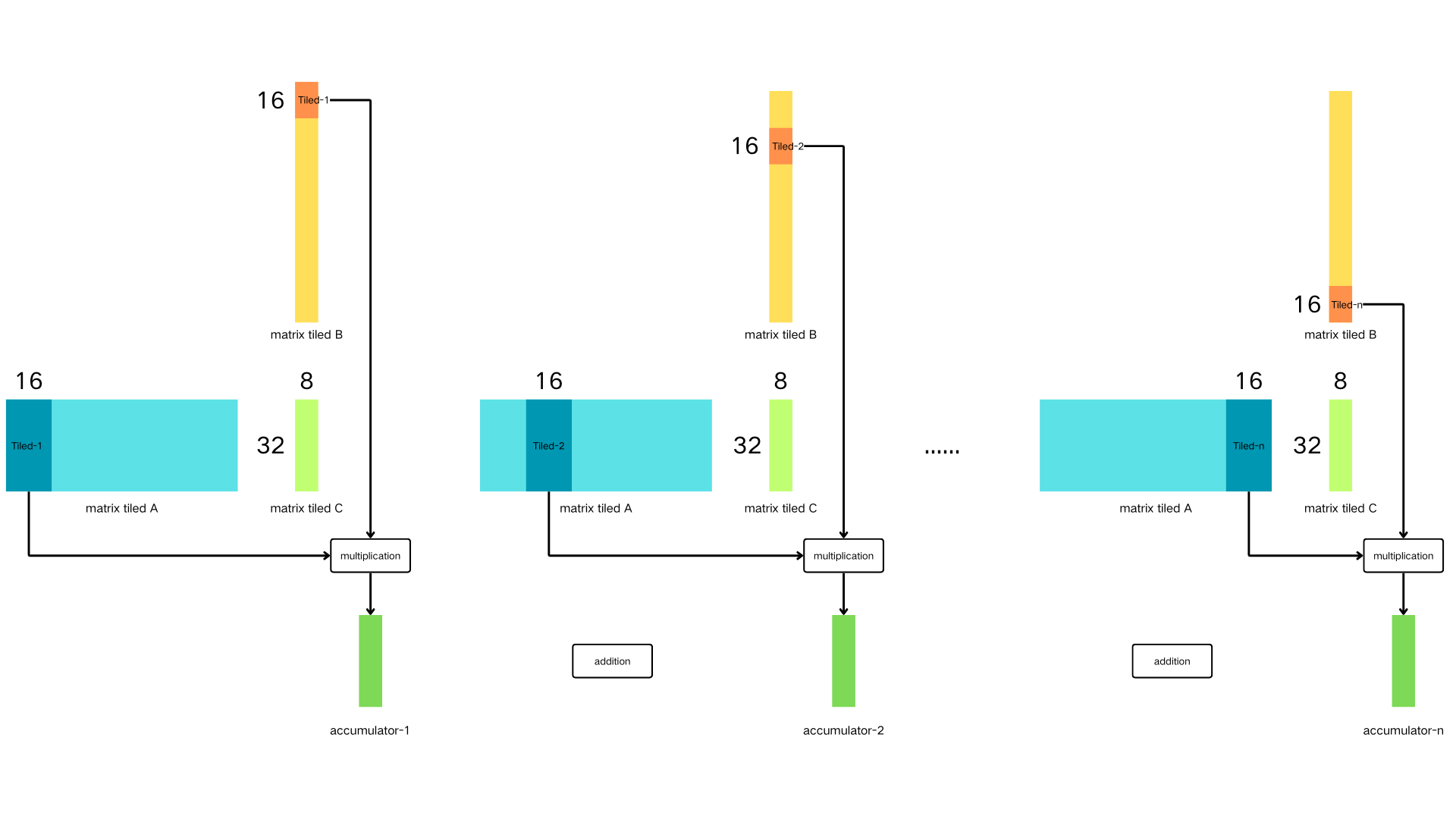
分块技术将 A, B 和 C 矩阵按照相对应的维度 (例如 C 块的维度是 m × n, A 块是 m × k, B 块是 k × n) 分为无数个小的矩阵块.
一个 m × n 的 C 块的结果由对应 m × k 的 A 块 和 k × n 的 B 块沿着 K 维相乘并累加得到.

如下图所示, 要计算一个 32 × 8 的 C 块, 它在结果矩阵 C 的位置是最左上角, 也就是由132行和18列组成的矩阵块.
设 k = 16, 则首先计算A矩阵的第031行和第015列组成的A块与B矩阵的第015行和第07列组成的B块相乘得到中间结果矩阵acc(
accumulator-1)块,
再计算由第031行和第1631列组成的A块与第1631行和第07列组成的B块相乘得到的新的acc(accumulator-2)块与上一次的acc(
accumulator-1)块做矩阵加法.
沿K维循环迭代进行, 最终遍历计算 A 矩阵第031行的所有数据和 B 矩阵第07列的所有数据得到最终结果矩阵 C 块.

分块矩阵相乘累加示例

使用分块技术来计算矩阵乘法最主要的操作就是两个矩阵块相乘, 将结果矩阵块累加到上一次的结果矩阵块.
Tensor core 就是用于计算矩阵相乘和累加的操作.

将矩阵按照 Tensor core 支持的矩阵维度来分块, 随后将 A 块 和 B 块利用 Tensor core 沿着 K 维相乘累加得到结果矩阵 C 块.
再进行同样的操作来计算下一个 C 块, 最后所有的 C 块结合起来得到最终的结果矩阵.

也可以通过使用 cuBLAS 和 cuDNN 这两个 CUDA 库来间接使用 Tensor Cores.
cuBLAS 利用 Tensor Cores 加速密集矩阵乘法(GEMM)计算;
cuDNN 则利用 Tensor Cores 加速卷积和循环神经网络(RNNs)的计算.

WMMA API

CUDA 9.0 引入了一个以 warp 级别进行操作的矩阵计算函数, 以便开发者可以使用 GPU 上的 Tensor Core.
称为WMMA(Warp-level Matrix Multiply and Accumulate)API.
通过 WMMA API, 可以将 D = A × B + C 运算使用 warp 级别进行操作,
其中的A、B、C、D都是更大矩阵的块(tile). 也就是可以使用一个 warp (32个线程) 来计算一个结果矩阵块.

实际工作中, 一个warp中的每个线程都只计算结果矩阵块的8个数据(16×16/32).

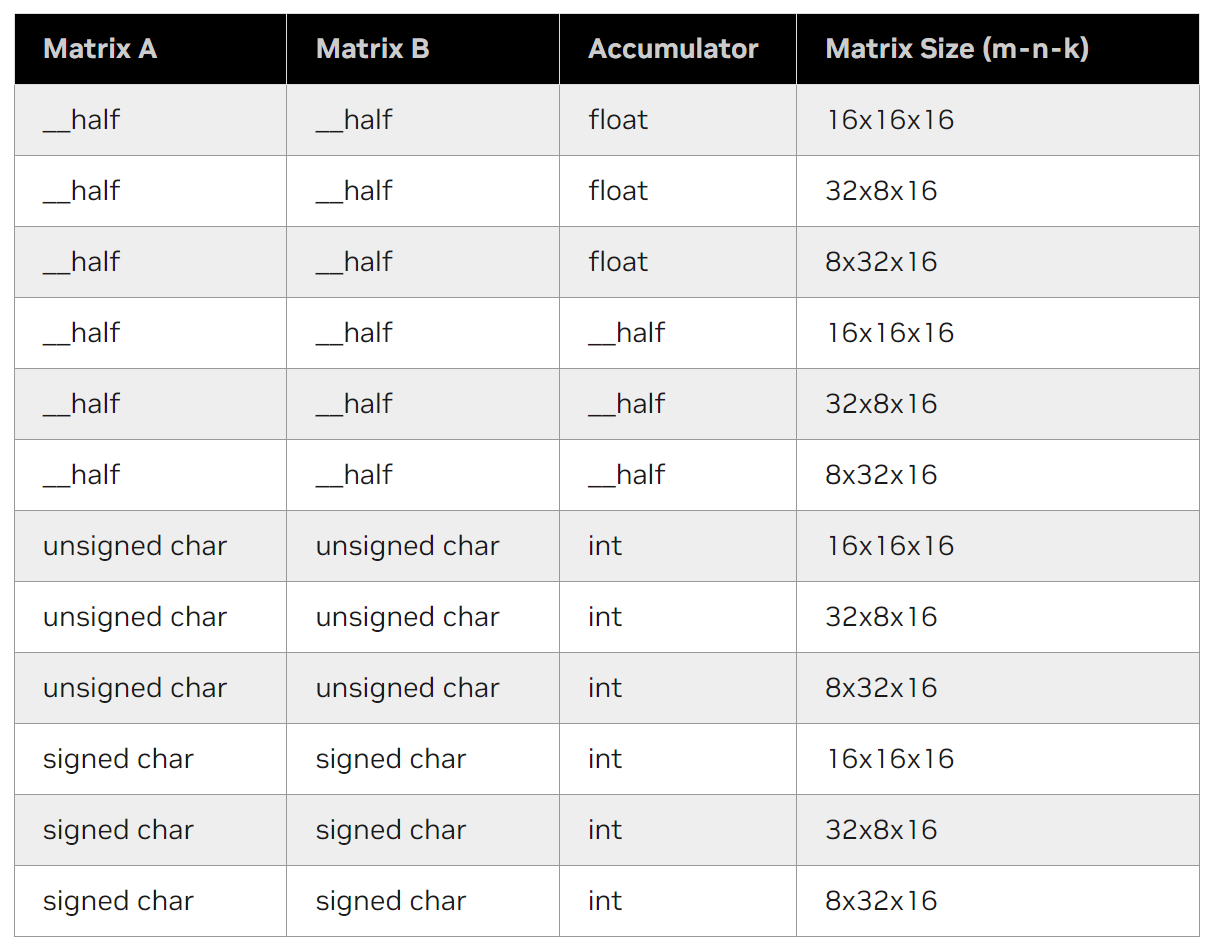
Tensor core 支持各种元素类型和矩阵维度, 下表列出了目前WMMA API支持的 matrix_a, matrix_b 和 accumulator 矩阵的部分格式和矩阵维度.

Tensor core WMMA API 目前支持的格式和矩阵维度

这里只列出部分常用格式.
Tensor core 还支持特殊格式, 详细可在官网查看 :
CUDA C++ Programming Guide 7.24.6. Element Types and Matrix Sizes

要通过 WMMA API 来使用 Tensor core 只需要简单4个步骤 :

• 首先创建用于储存矩阵块的 fragment 类
• 将矩阵块读取到 fragment 类中
• 进行矩阵乘法累加计算
• 最后将计算结果写回到结果矩阵

调用前需要检查 GPU 是否带有 Tensor core, 并且在构建项目时设置对应的 GPU 架构.
构建方式可以查看另一篇文章 : 用 CMake 构建跨平台 CUDA C/C++ 项目

WMMA API的所有函数和类型都在头文件 mma.h 中的 namespace::nvcuda::wmma 命名空间中定义.
为了简化代码的同时避免命名空间冲突, 保持 wmma 的显示, 只使用 nvcuda 命名空间.

#include <mma.h>
using namespace nvcuda;

fragment 类

fragment 是一个重载类, 用于储存矩阵片段(块)的数据.

template<typename Use, int m, int n, int k, typename T, typename Layout=void> class fragment;

// examples
wmma::fragment<wmma::matrix_a, WMMA_M, WMMA_N, WMMA_K, half, wmma::row_major> aFrag;
wmma::fragment<wmma::matrix_b, WMMA_M, WMMA_N, WMMA_K, half, wmma::col_major> bFrag;
wmma::fragment<wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> cFrag;

• Use : 用作第一个乘数的矩阵使用 matrix_a , 第二个乘数的矩阵使用 matrix_b . 当分别用作累加器C或目标累加器D时使用
  accumulator
• m , n , k : 表示参与乘法和累积操作的矩阵块的形状, 比如说矩阵A块是m×k, 矩阵B块是k×n, 矩阵C块是m×n
• T : 使用的数据类型. double , float , __half , __nv_bfloat16 , char , unsigned char
• Layout : 表示矩阵是以行主序 row_major 或列主序 col_major 的形式保存在内存中, 当 Use 参数使用 accumulator
  时则不需要填写,
  默认是列主序储存

成员变量 num_elements 记录元素总数, 一般为8. 配合成员变量 x 可以遍历所有元素. 例如让储存的所有元素乘2 :

for (int idx = 0; idx < frag.num_elements; ++idx) {
    frag.x[idx] *= 2;
}

官方文档(CUDA C++ Programming Guide)中关于fragment类的描述说 "The mapping of matrix elements into fragment internal
storage is unspecified and subject to change
in future architectures."
也就是说通过以上方式不能准确知道遍历过程中当前 idx 下的 frag.x[idx] 在实际矩阵块中的哪个位置.

但是实际可以直接通过将同一个warp中的每个线程(lane)储存的元素全部打印出来对照查看就能知道.
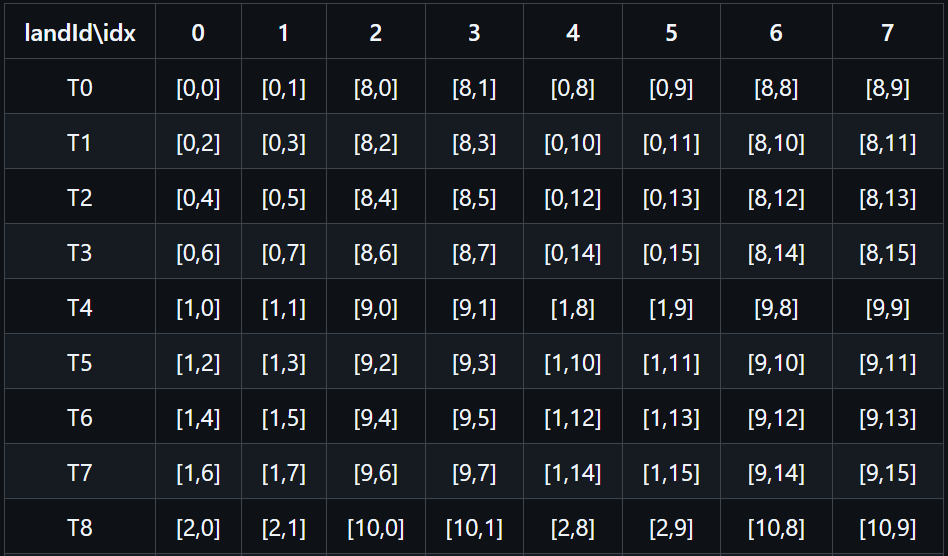
以下列表是当m,n,k都分别设置为16的情况下每个线程储存原始矩阵的位置.

Warp是CUDA中最小的执行单元, 它由一组固定数量的线程组成(在NVIDIA的Fermi架构及以后的GPU中, 一个warp包含32个线程).
同一个warp中, 每个线程被称为一个"lane", 术语来自于"车道"的比喻, 就像在高速公路上, 每个车道可以独立行驶一辆车.
每个lane可以看作是一个独立的执行路径, 它们共享warp的执行状态, 但各自有自己的寄存器和执行流.

m16n16k16情况下, 部分线程fragment类中储存的原矩阵块C的元素位置. 行标为laneId, 列标为fragment类的Index. 数据为[row,col]

通过上图可以发现一些规律:

1. 从每个线程储存的行数上看, 线程的每两个Index储存相同的行元素, 并且Index为01和45储存了相同的行元素, 23和6
   7储存了相同的行元素. 也就是每个线程只储存了两个行元素, 并且相差为8, 01和45是小一些的行数.
2. 从每个线程储存的列数上看, 线程的每两个Index储存连续的两列元素, 并且Index为0和2储存了相同的列元素, 1和3储存了相同列元素.
   也就是每个线程储存了4个列元素, 并且每两个列元素相差为8, 前4个Index储存了小一些的列数.
3. 从每个线程储存的列数与Index对比, 发现Index为偶数时, 储存的列数也为偶数, Index为奇数时, 储存的列数也为奇数.
4. 原矩阵同一行的数据由每连续的4个线程储存.
5. 0到15行数据中, 行数以8为分界线, T0储存第0行和第8行的元素, 之后根据规律③增加.
6. 0到15列数据中, 列数以8为分界线, 每个线程的每两个Index储存连续的2列的元素. 根据规律③的4个线程为一组, 组内第0号线程,
   储存0,1,8,9列元素, 第1号线程储存2,3,10,11列元素, 以此类推.

例如要找到原矩阵块中第1行第12列的是在哪个线程储存, 储存的Index是多少?
可以先通过行数, 根据第④和第⑤条规律计算出从哪个线程ID开始储存.

const int startLane = localRow % 8 * 4;

从以上公式算出[1,12]是由第4号开始的线程储存, 也就是4~7线程储存了第1行元素.

再通过列数, 根据第④和第⑥条规律计算出在连续四个线程中的哪个线程储存了该元素. 最终得到线程(lane)ID.

laneId = startLane + localCol % 8 / 2;

从以上公式算出[1,12]是由第6号线程储存. 知道了线程Id之后还需要知道属于fragment类中的哪个Index储存.

最后根据第①, ②和③条规律计算出元素所在fragment类中的Index.

const int isBigRow = localRow / 8;
const int isBigCol = localCol / 8;
index = isBigCol * 4 + isBigRow * 2 + localCol % 2;

最终得到第1行第12列的数据由fragment类的Index为4的第6号线程储存.

以上规律虽然说可能会在未来的架构中改变, 但是在短时间内大概率不会进行更改. 并且未来更改了也可以根据这样的方式找到计算的方法.

加载矩阵数据

load_matrix_sync() 函数用于从内存加载矩阵的片段到 fragment 类中. 并且开始前会进行线程同步(sync)操作.

void load_matrix_sync(fragment<...> &a, const T* mptr, unsigned ldm);
void load_matrix_sync(fragment<...> &a, const T* mptr, unsigned ldm, layout_t layout);

• a : 函数输出. 储存矩阵片段的 fragment 类
• mptr : 必须是一个 256 位对齐的指针, 指向内存中矩阵第一个要加载的元素
• ldm : 表示元素在连续行(行主序时)或列(列主序时)在内存中的跨度. 也就是每行/列的元素数量
• layout : 指定矩阵是以行主序或列主序的形式保存在内存中, 必须指定为行主序 : mem_row_major 或列主序 : mem_col_major

注意 : 因为会进行线程同步操作, 此函数必须由 warp 中的所有线程调用.

如果要加载的块不满足对应的矩阵维度, 结果将出错. 也就是说要保证输入矩阵块的大小和 fragment 类的参数相匹配.
例如指定的fragment类的m,n,k分别为32,8,16, 那么加载的矩阵块A的大小必须是32×16, 矩阵块B的大小必须是16×8.

特别是在进行K迭代时, 要注意是否超过了原始矩阵的大小.

矩阵计算

mma_sync() 函数进行矩阵乘法累加计算. 会在开始前进行线程同步(sync)操作.

void mma_sync(fragment<...> &d, const fragment<...> &a, const fragment<...> &b, const fragment<...> &c, bool satf=false);

• d , a , b , c : 表示对应的矩阵片段
• satf : 饱和有限值模式, 也就是安全模式. 默认为 false , 如果设置为 true , 则目标累加器有以下额外的数值属性 :
  • 如果一个元素的计算结果为正无穷, 则对应的累加器将会包含 +MAX_NORM
  • 如果一个元素的计算结果为负无穷, 则对应的累加器将会包含 -MAX_NORM
  • 如果一个元素的计算结果为 NaN, 则对应的累加器将包含 +0

矩阵之间片段的形状必须匹配, 也就是参数 m , n , k 需要相匹配.

将 A 块和 B 块相乘, 结果累加到 acc 块中 :

mma_sync(accFrag, aFrag, bFrag, accFrag);

注意 : 因为会进行线程同步操作, 此函数必须由 warp 中的所有线程调用.

存储矩阵数据

store_matrix_sync() 函数与 load_matrix_sync() 函数相反, 是将矩阵片段存储回内存中. 也会在开始前进行线程同步(sync)操作.

void store_matrix_sync(T* mptr, const fragment<...> &a, unsigned ldm, layout_t layout);

• mptr : 必须是一个256位对齐的指针, 指向数据储存的第一个位置
• a : 源矩阵片段 fragment 类
• ldm : 表示元素在连续行(行主序时)或列(列主序时)在内存中的跨度. 也就是每行/列的元素数量
• layout : 指定矩阵是以行主序或列主序的形式保存在内存中, 必须指定为行主序 mem_row_major 或列主序 mem_col_major

注意 : 因为会进行线程同步操作, 此函数必须由 warp 中的所有线程调用

填充矩阵数据

fill_fragment() 是用于对矩阵片段 fragment<> 类进行操作, 可以用常量值 v 来填充整个矩阵片段.

void fill_fragment(fragment<...> &a, const T& v);

一般用于对创建的 fragment 类进行初始化, 例如将记录中间结果的 acc 块先初始化为 0 :

wmma::fragment<wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> accFrag;
wmma::fill_fragment(accFrag, 0.0f);

cuBLAS 库使用 Tensor core

使用 cuBLAS 库先要创建...........
目前只有 GEMM 操作支持使用 Tensor core, 要使用 Tensor core 需要设置数学模式为 : CUBLAS_TENSOR_OP_MATH .

cublasSetMathMode(cublasHandle, CUBLAS_TENSOR_OP_MATH);

A, B 和 C 矩阵都默认为列主序储存

参数:

• CUBLAS_OP_N : 非转置操作
• CUBLAS_OP_T : 转置操作
• CUBLAS_OP_C : 共轭转置操作

共轭转置 : 要理解共轭转置首先要了解什么是实数什么是虚数.
实数是可以在数轴上面表示的数, 也就是平常接触到的数, 可以进行标准的加减乘除操作.
复数是由实数和虚数部分组成的数, 基本形式为 a + b * i ,
其中 a 是实部(可以是任何实数), b 是虚部(可以是任何实数), i 是虚数单位(满足 i² = -1 ).
实数是复数的一个子集(也就是 b = 0 时). 复数在实数系统中无法表示,
复数的引入扩展了数学的边界, 使得能够解决一些在实数范围内无法解决的问题.
而共轭转置就是将一个复数 a + b * i 变为 a - b * i

示例

下面是使用WMMA API计算稠密矩阵-稠密矩阵乘法的示例. 其中矩阵A和矩阵B的类型为half, 结果矩阵C的类型为float.
矩阵块维度m,n和k都是16. 所有矩阵都以行主序储存.

// According to the planning of cuda thread blocks, 
// calculate the row id and column id of the resulting matrix block C to be computed by the current warp.
int cRow, cCol;

wmma::fragment<wmma::matrix_a, WMMA_M, WMMA_N, WMMA_K, half, wmma::row_major> aFrag;
wmma::fragment<wmma::matrix_b, WMMA_M, WMMA_N, WMMA_K, half, wmma::row_major> bFrag;

wmma::fragment<wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> accFrag;
fill_fragment(accFrag, 0.0f);

// All matrices are stored in row-order
const int lda = K;
const int ldb = N;
const int ldc = N;

for (int kIter = 0; kIter < K; kIter += WMMA_K) {
const int aRow = cRow;
const int aCol = kIter;

const int bRow = kIter;
const int bCol = cCol;

// bounds checking
if (aRow < M && aCol < K && bRow < K && bCol < N) {
const half* aOffsetPtr = mtrA + aRow * lda + aCol;
const half* bOffsetPtr = mtrB + bRow * ldb + bCol;

load_matrix_sync(aFrag, aOffsetPtr, lda);
load_matrix_sync(bFrag, bOffsetPtr, ldb);

mma_sync(accFrag, aFrag, bFrag, accFrag);
}
}

float* cOffsetPtr = mtrC + cRow * ldc + cCol;

store_matrix_sync(cOffsetPtr, accFrag, ldc, wmma::mem_row_major);

参考:

[1] Tips for Optimizing GPU Performance Using Tensor Cores

[2] CUDA C++ Programming Guide:7.24. Warp Matrix Functions

[3] NVIDIA TESLA V100 GPU ARCHITECTURE

[4] PTX ISA 8.5: 9.7.15.4.1. Matrix Fragments for mma.m8n8k4 with .f16 floating point type