论文封面

[论文笔记]深度学习中N:M稀疏权重的高效GPU内核

EFFICIENT GPU KERNELS FOR N:M-SPARSE WEIGHTS IN DEEP LEARNING

论文于2023年发表在Sixth Conference on Machine Learning and Systems · Miami (MLSys 23).

在深度学习领域中,N:M稀疏性越来越受欢迎. 但因为缺乏针对各种稀疏比的通用GPU kernel库,论文介绍了一个高效GPU kernel库: nmSPARSE. 用于具有N:M稀疏权重的神经网络的两种基本操作:稀疏矩阵-向量乘法(SpMV)和稀疏矩阵-矩阵乘法(SpMM).

论文主要探讨针对N:M稀疏性的稀疏矩阵-向量乘法和稀疏矩阵-矩阵乘法的GPU加速. 下面先介绍什么是权重剪枝和N:M稀疏性.

文章链接 : [论文笔记]深度学习中N:M稀疏权重的高效GPU内核

Weight Pruning

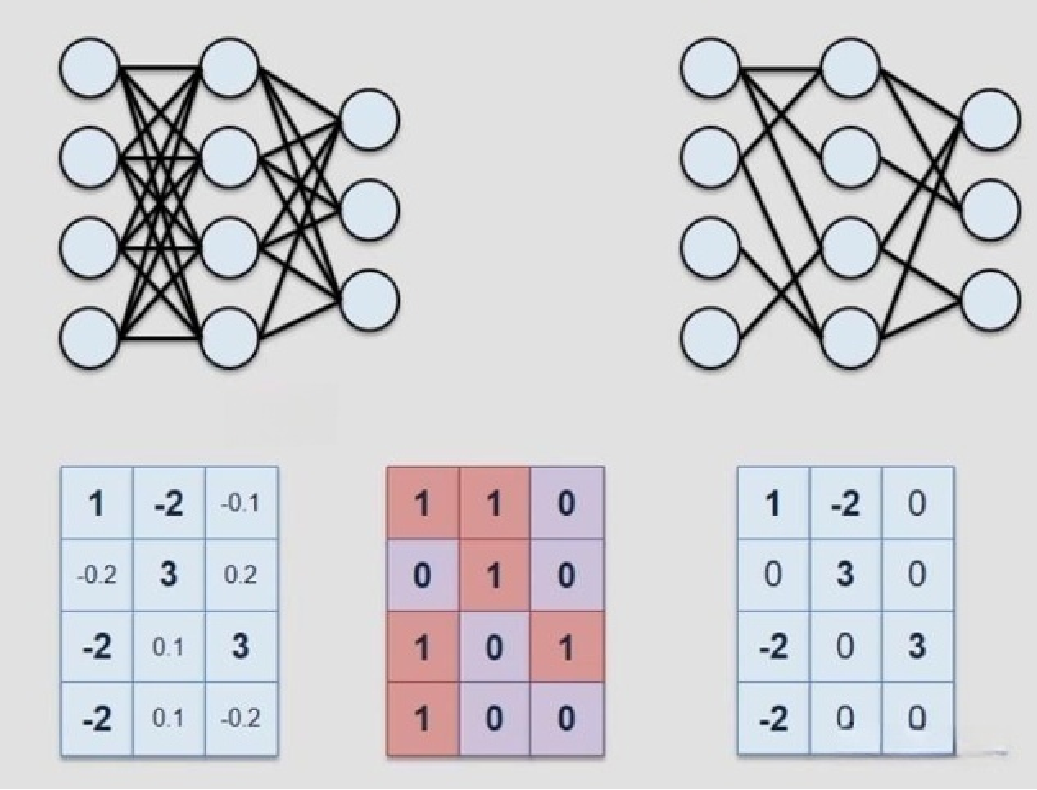
为了减少深度神经网络(DNN)的模型大小并加速模型推理, 权重剪枝(Weight Pruning)算法在学术界和工业界得到广泛的研究.

权重剪枝的目的是找到并去除对模型精度影响不大的冗余权重. 从而直接减少了模型的内存占用和计算规模.

如图所示,图中占比重要的权重被保留,冗余的权重被去除.在保留模型精度的同时降低了计算规模

如图所示, 图中占比重要的权重被保留, 冗余的权重被去除. 在保留模型精度的同时降低了计算规模.

通过调整权重剪枝(Weight Pruning)算法可以将权值修剪为N:M稀疏模式, 随着权值被修剪为稀疏后, DNN推理中最频繁和耗时的稠密矩阵-向量乘法(GEMV)和稠密矩阵-矩阵乘法(GEMM)变为了具有N:M稀疏性的稀疏矩阵-向量乘法(SpMV)和稀疏矩阵-矩阵乘法(SpMM). 那么什么是N:M稀疏性呢?

N:M sparsity

N:M稀疏性可以为深度学习提供高模型精度和计算效率.

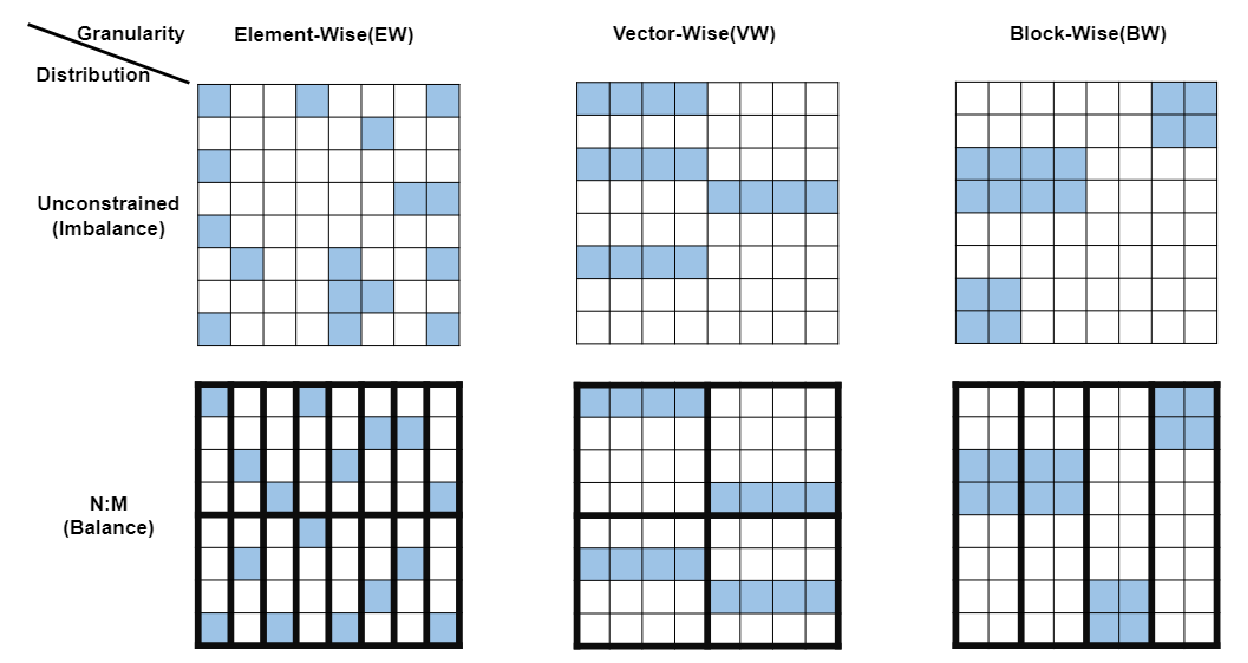
N:M稀疏性本质上对非零权重施加了平衡分布,具体为每连续的M个权值中,只有N个权值不为零.

三种稀疏模式

图上展示了三种稀疏模式, 元素型, 矢量型和块型. 图中蓝色方块代表非零值, 白色方块代表0. 上面一列是无约束分布的数据, 下面一列是N:M平衡分布的数据. 图中稀疏比为1:4. 左下角的图表示垂直的每四个权值中有一个非零权值.

注意,N:M分布是沿着矩阵乘法中的降维k分布的
N:M稀疏性只限制了非零元素的局部分布,每个M大小的窗口中的分布不受限制.所以对模型精度的影响很小.同时N:M稀疏性在GPU上实现高效并行执行方面有很大的潜力.

N:M sparsity压缩表示

稀疏矩阵有各种压缩表示格式,如CSC,CSR,COO等.

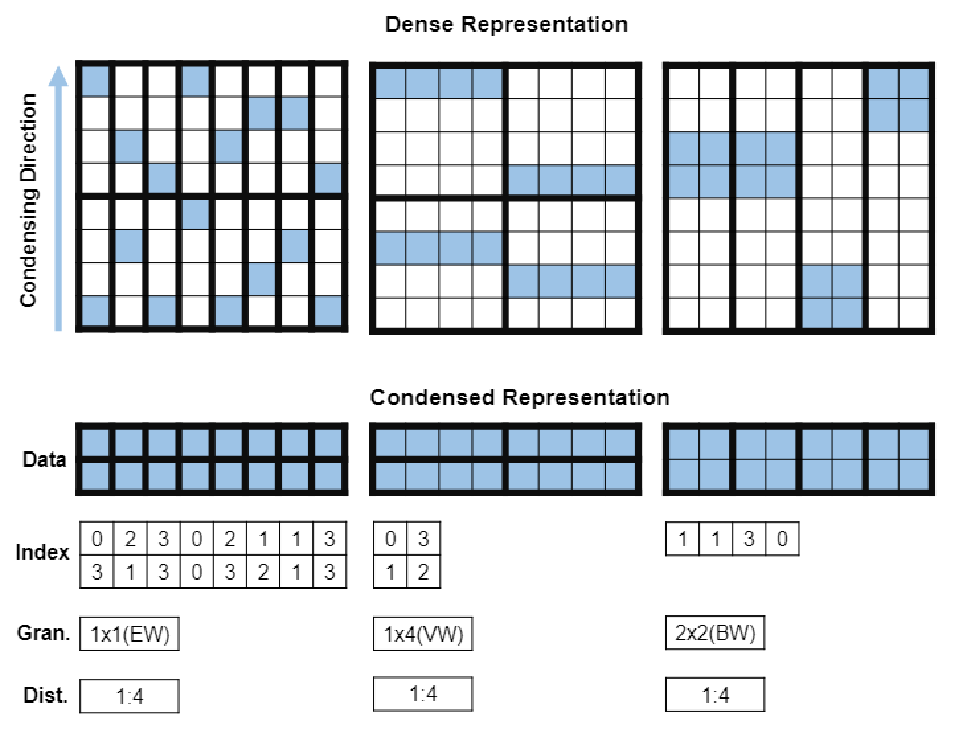
论文中给出专用于nmSPARSE中N:M稀疏模式的压缩表示格式.

EW-/VW-/BW-N:M sparsity的数据压缩表示

EW-/VW-/BW-N:M sparsity的数据压缩表示.

如图,将非零数据按竖直方向压缩后,创建一个大小相同的位置数组记录对应非零数据在原矩阵中M窗口中的位置索引. 并记录稀疏模式和稀疏比.

nmSPARSE库

论文介绍的nmSPARSE是一个高效的GPU kernel库,用于N:M稀疏权重的神经网络中的两种基本操作:稀疏矩阵-向量乘法(SpMV)和稀疏矩阵-矩阵乘法(SpMM).

并基于ASP算法(由Nvidia开发用于生成稀疏网络的开源Pruning库), 做出三个扩展:

  1. 支持任意N:M设置. 意味着支持生成任意N:M稀疏比
  2. 扩展ASP支持nmSPARSE的VW/BW-N:M稀疏模式
  3. 进一步启用分层稀疏比配置

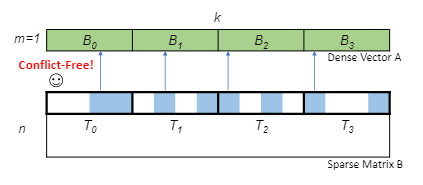
值得一提的是在实现nmSPARSE的SpMV和SpMM kernel时利用了共享内存的无冲突访问模式(conflict-free access)和无冲突广播访问模式(conflict-free broadcast access).

下面介绍什么是共享内存的无冲突访问模式(conflict-free access)和无冲突广播访问模式(conflict-free broadcast access).

共享内存:无冲突访问(conflict-free access)

共享内存是一个可以被同时访问的一维地址空间.
共享内存中被分为32个同样大小的存储体(bank)，对应线程束中32个线程.

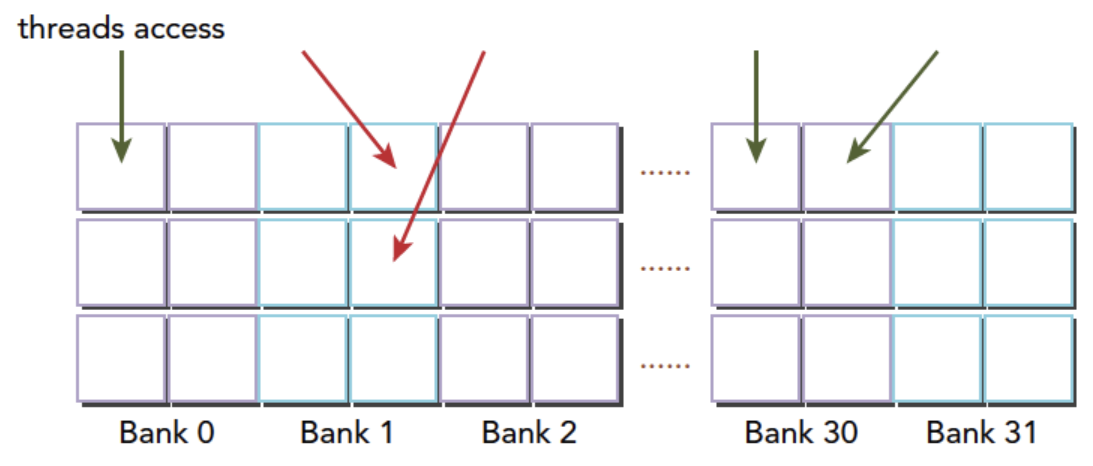
在共享内存中当多个地址请求落在相同的内存库的不同地址中时， 就会发生存储体冲突(bank conflict)， 这会导致请求被重复执行, 从而降低带宽.

多个线程同时访问同一个bank. 图片来自谭升的博客

多个线程同时访问同一个bank产生bank conflict. 图片来自谭升的博客.

这里对于bank conflict不做深入的介绍,具体可以参考这个链接的文章:共享内存之bank冲突

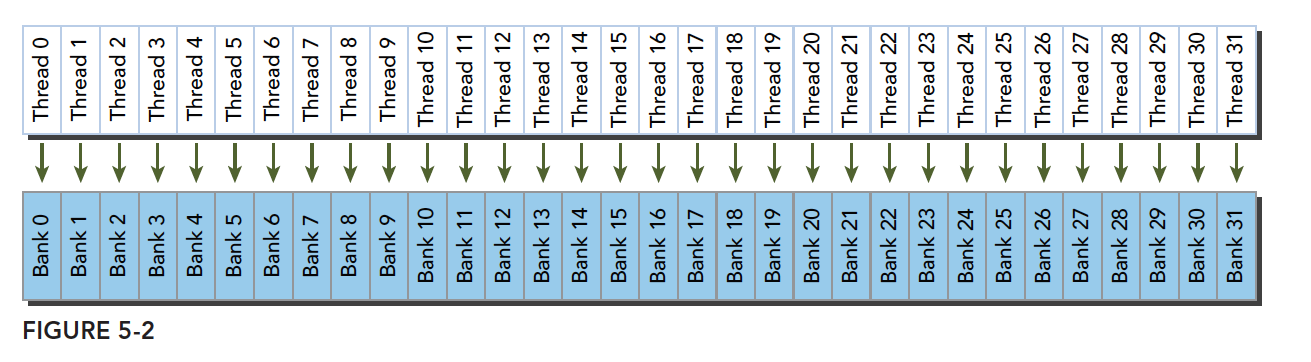
相反,如果warp中的32个线程的内存访问映射到32个不同的存储体,那么可以同时提供服务,不会产生bank冲突,这种模式也被称为无冲突访问模式(conflict-free access)

每个线程都访问不同的bank. 图片来自谭升的博客

最理想的访问模式, 每个线程都访问不同的bank. 图片来自谭升的博客.

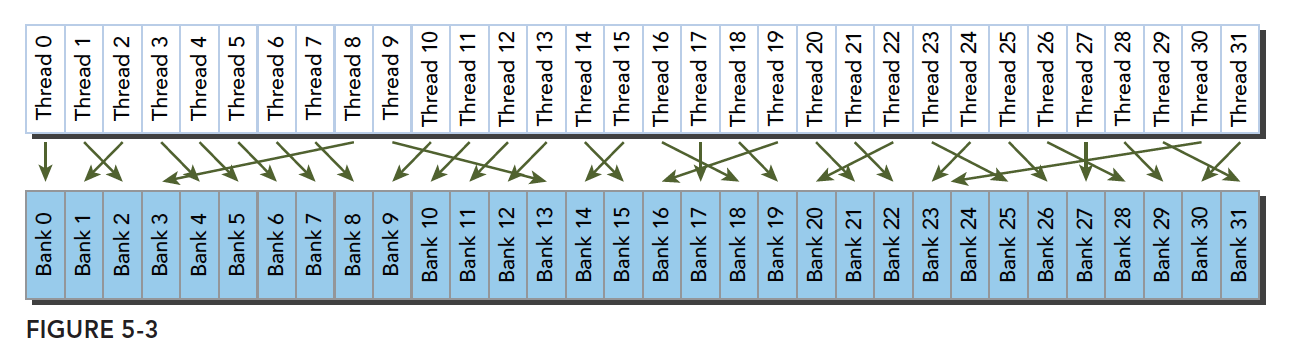
当然不规则访问的同时访问不同的bank也属于无冲突访问模式(conflict-free access)

不规则访问的无冲突访问模式(conflict-free access). 图片来自谭升的博客.

共享内存:无冲突广播访问(conflict-free broadcast access)

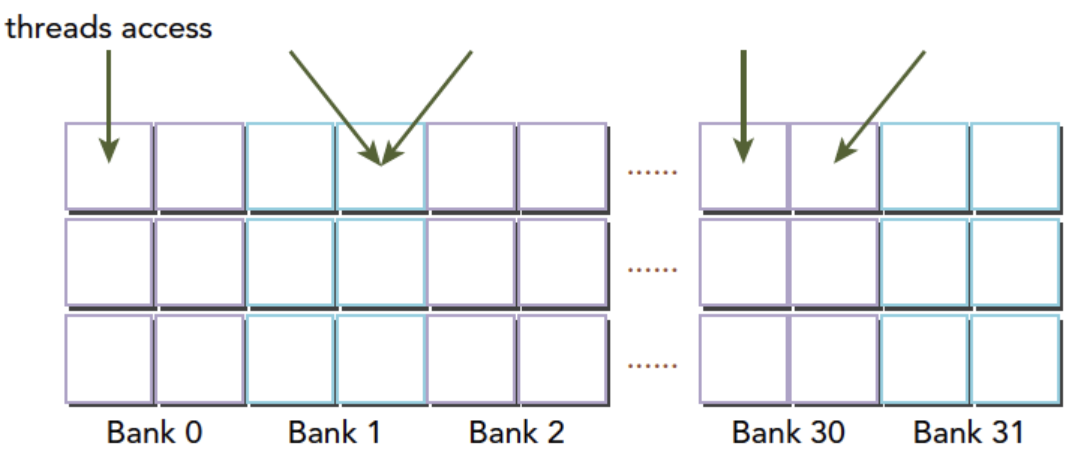
当一个warp中的多个线程访问同一个bank,但是使用的是完全相同的地址时,可以通过硬件支持的广播机制来提供服务,不会出现存储体冲突(bank conflict).这种访问模式称为无冲突广播访问模式(conflict-free broadcast access).

上图两条红色的线访问了同一个bank1的不同地址, 出现了bank冲突.

如上图, 虽然有两个线程都访问了同一个bank1,但是访问的是完全相同的地址.这种访问模式就称为无冲突广播访问模式(conflict-free broadcast access).

nmSPARSE: SpMV kernel的无冲突访问

  1. nmSPARSE的SpMV kernel进一步将每个稀疏列划分为大小为M的子列.
  2. 每个线程计算稀疏矩阵的一个子列的点积.
  3. 因为每M个元素中只有N个非零元素,所以每个线程的工作负载是平衡的.
  4. 稠密向量A则从全局内存加载到共享内存中,并且根据每个子列需要的向量划分到不同的内存块中.
  5. 不同线程只需要访问不同的内存块,消除了bank冲突.

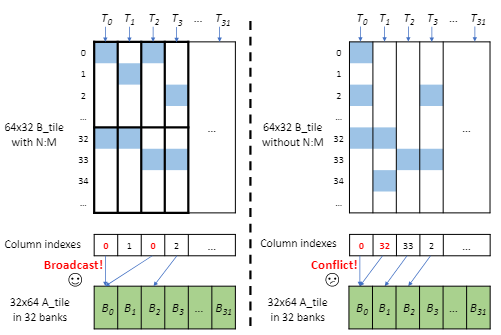
各个线程访问不同的储存库,例如线程T0访问bank0,线程T1访问bank1

nmSPARSE: SpMM kernel的无冲突广播访问

nmSPARSE中的SpMM kernel将稠密矩阵A储存在共享内存中,将线程映射到稀疏矩阵B中的列来实现对A中所需元素的访问

  1. 通过将稠密A矩阵按行储存在共享内存中,如图A矩阵一行有32个元素,一行的元素刚好可以对应储存同在一个bank.
  2. 每个线程负责稀疏B矩阵的每一列.
  3. 由于N:M稀疏模式按列的内部平衡分布,所以每个线程的工作负载是平衡的.
  4. 在同一个warp中的两个线程访问同一块内存中完全相同的地址,可以运用广播机制完美解决这个冲突.

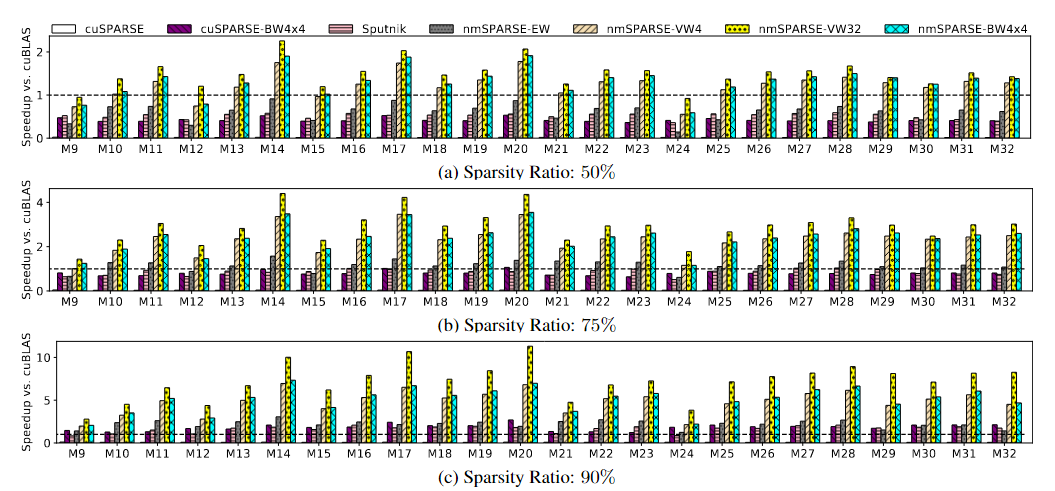
nmSPARSE性能测试

通过与当前最先进的稠密和稀疏库以及DNN编译器进行比较，在操作基准和端到端模型上评估nmSPARSE内核。

研究结果如下：

  1. nmSPARSE的EW-N:M内核在SpMV和SpMM算子上分别比最快的基准实现了5.2倍和2.1倍的加速。
  2. 随着粒度的增加，nmSPARSE内核在SpMM算子上可以比最快的基准实现高达6.0倍的加速。
  3. 对Transformer的端到端研究表明，nmSPARSE优于其他基准。

nmSPARSE在CUDA核心上针对不同大小的SpMV算子的加速结果

nmSPARSE在CUDA核心上对不同大小的SpMM算子在50%,75%,90%稀疏率下的加速结果

nmSPARSE在CUDA核心上对不同大小的SpMM算子在50%,75%,90%稀疏率下的加速结果

结语

论文结合GPU共享内存的优势和N:M稀疏性的平衡分布,设计并实现了调度内存请求的SpMV内核和SpMM内核, 以消除共享内存中的bank冲突. 解决了稀疏矩阵乘法中不规则的计算和分散的内存访问问题.

在阅读完本篇论文并做完课上的论文发表后,想着心思都花了不如整理下来方便以后翻看.

在阅读论文和准备论文发表时也查阅了许多文献, 文中可能有抄录的地方, 但是现在也很难找到原文链接.希望原作者理解.

可能有理解或表述不当的地方, 欢迎大家指正.

论文链接:Efficient GPU Kernels for N:M-Sparse Weights in Deep Learning

❤️ 转载文章请注明出处，谢谢！❤️