[论文笔记]用于高性能机器学习的抽样稠密矩阵乘法

Sampled Dense Matrix Multiplication for High-Performance Machine Learning

论文于 2018 年发表在 IEEE 25th International Conference on High Performance Computing (HiPC).

论文详细介绍了采样稠密-稠密矩阵乘法(SDDMM) 作为许多机器学习因子分析算法（如 Alternating Least Squares (ALS)、Latent Dirichlet Allocation (LDA)、Sparse Factor Analysis (SFA) 和 Gamma Poisson (GaP)）的核心组件. SDDMM 需要计算两个输入稠密矩阵的乘积，但仅在结果矩阵中对应于第三个输入稀疏矩阵的非零位置处进行计算. 论文还介绍了 cuSDDMM，这是一个多节点 GPU 加速的 SDDMM 实现，相对于当前最佳的 GPU 实现（在 BIDMach 机器学习库中）具有最高4.6倍的加速效果.

文章链接 : [论文笔记]用于高性能机器学习的抽样稠密矩阵乘法

Sampled Dense-Dense Matrix Multiplication

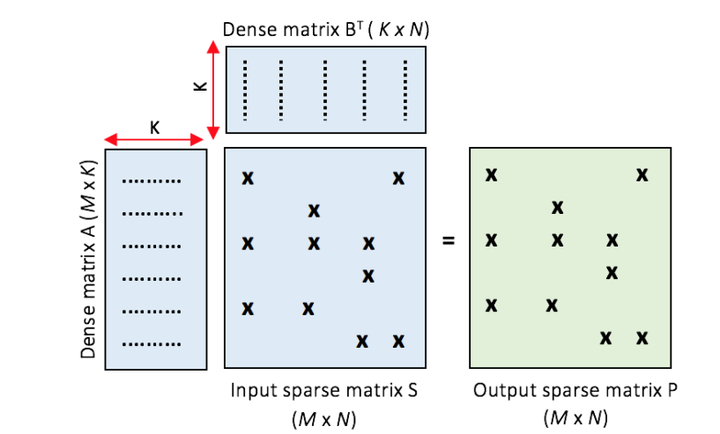
采样稠密-稠密矩阵乘法(SDDMM)具有一个稀疏矩阵和两个稠密矩阵作为输入,一个稀疏矩阵作为输出. 采样指的是对两个稠密矩阵乘法的结果矩阵中随机保留一些元素. SDDMM计算两个稠密输入矩阵的乘积, 但仅根据输入稀疏矩阵对应的非零位置处进行计算.

在几种ML算法中(如交替最小二乘(ALS)), SDDMM内核在计算上占主导地位(占总执行时间的65%), 优化SDDMM算法可以提高几种ML算法的性能.

SDDMM示例:在稀疏矩阵S中非零位置的元素累积稠密矩阵A和B的乘积,生成输入稀疏矩阵P.

在矩阵乘法中处理大规模稠密矩阵时, 计算复杂度和内存开销是主要挑战. 采样技术通过选择矩阵中的一部分元素进行计算, 从而有效降低计算量.

SDDMM可以使用A和B之间的高效稠密矩阵乘法(DGEMM)执行,然后提取采样元素. 但是这样会产生大量不必要的计算. 通过只执行与非零元素对应的计算,计算复杂度可以从O(K.M.N)降低到O(K.nnz)(nnz:number of non-zero).

与研究较多的优化SpMV(稀疏矩阵向量积)问题相比, SDDMM具有一个输入稀疏矩阵和两个输入稠密矩阵, 因此在为GPU设计有效并行实现时,需要考虑更多的数据访问. 而且与内存带宽严重受限的SpMV不同的是, SDDMM的每个输入稀疏矩阵的元素都会乘以两个稠密输入矩阵的向量的点积, 具有很多可以合并的内存访问. 因此与SpMV相比, SDDMM显著提高了Roofline性能极限.

Roofline模型是关注算力和带宽来研究和分析程序运行的瓶颈, 具体可以参考这个文章: Roofline Model与深度学习模型的性能分析

cuSDDMM

论文介绍的cuSDDMM是一种SDDMM的多节点GPU加速实现. 通过分析SDDMM的数据重用特征给出了两种解决方案. SM-SM(Shared memory-Shared memory)方案和SM-L2(shared memory-L2 cache)方案.

在GPU加速优化中, 对于数据重用的情况, 利用共享内存来加速是一个很常用方法. 共享内存访问的低延迟和高带宽可以很好地优化数据重用. 对于共享内存的详细介绍可以查看这个博客: 【CUDA 基础】5.1 CUDA共享内存概述

SM-SM方案

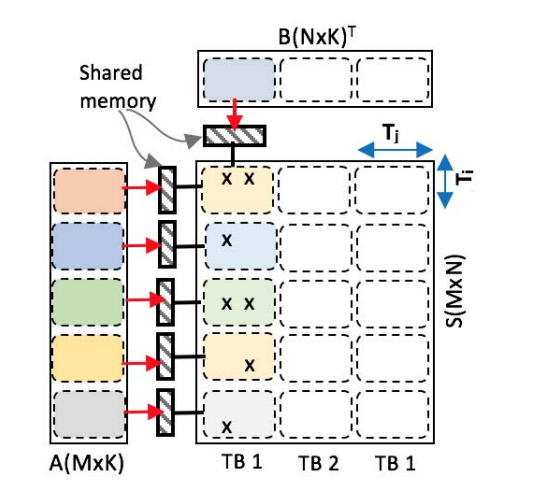
SM-SM(Shared memory-Shared memory)方案通过将A和B两个矩阵加载到共享内存来消除未合并的全局内存访问.

共享内存的延迟大约比全局内存访问低100倍

但由于共享内存大小的限制, A片和B片的体积应该小于共享内存容量, 这限制了每个线程块的工作量.

SM-SM方案:每个线程块根据其共享内存容量将A片和B片加载到GPU的共享内存中.

如果稀疏矩阵的密度高, 那么A和B矩阵都能得到很好的重用, 这个方案会有很好地表现. 但由于共享内存大小的限制, A片和B片能存放在共享内存上的体积并不多. 每个稀疏矩阵的一个瓦片(tiled)分配给一个CUDA线程块, 然而A片和B片的大小限制了瓦片(tiled)的大小. 如果瓦片中没有包含足够的工作量(非零数据). 许多线程就会处于空闲状态, 从而降低性能.

实验结果显示如果稀疏矩阵密度≥5%时, 该方案明显优于 SM-L2 方案.

GFLOPS（Giga Floating Point Operations Per Second）是一个衡量计算设备性能的指标, 常用于描述CPU和GPU的性能. 它表示每秒能够执行的十亿次浮点运算次数.

SM-L2方案

SM-L2(shared memory-L2 cache)方案将其中一个稠密矩阵储存在共享内存中, 再利用L2缓存进行数据重用, 根据L2缓存容量来调整用于在一个线程块上计算的矩阵的大小.

![SM-L2 方案的分块和不分块的版本](/img/[论文笔记]用于高性能机器学习的抽样稠密矩阵乘法/SM-L2 方案的分块和不分块的版本.PNG)

SM-L2 方案的分块和不分块的版本. (a) 非分块: 矩阵A加载到共享内存中, 矩阵B依赖L2缓存进行数据重用. (b) (c) 分块: 将B矩阵分成两个瓦片分别进行计算. 在单个GPU上时,块1和块2按顺序执行, 在多GPU节点上时并行执行.

分块(tiling): 指的是将大数据集（如矩阵）划分为较小的块(或称为瓦片). 这些小块的大小通常与GPU的共享内存大小相匹配，以便可以完全加载到共享内存中. 是常用的优化技术.

在实际应用中, 实值矩阵通常表现出一种幂律结构特征, 即大多数行（或列）包含的非零元素数量很少, 而只有少数行（或列）包含大量的非零元素. 通过分块（tiling）处理数据时, 分块会增加在某个块(tiled)中出现空行的概率. 每个CUDA线程块在处理一个块(tiled)时，会将A矩阵中的连续行（即使是未使用的行）加载到共享内存中, 这样会导致某个时间步骤中可用的工作量受到限制. 为了缓解这个问题, 为每个块(tiled)维护一个"活跃行"的列表, 只将需要计算的行加载到共享内存中进行处理.

在SM-L2方案的实现中, 每个线程块使用SM上可用共享内存的一半, 只有两个线程块可以同时活动. 为了最大化占用, 每个线程块分配1024个线程(单个线程块所能分配的最大线程数). 但是因为输入矩阵非常稀疏, 导致每个线程块能处理的元素少于1024个, 如果按照一个元素分配给一个线程计算, 则会有一些线程无事可做. 为了解决这个问题, 可以让单个元素分配给多个线程进行计算, 增加并行度. 这种情况则需要归约操作来合并多个线程计算的结果, 使用warp shuffle可以高效地完成这个工作.

warp shuffle作用在一个线程束内, 允许两个线程间相互访问对方的寄存器, 并且延迟极低, 不消耗内存. shuffle指令是线程束内线程通讯的极佳方式. 关于shuffle 具体可以参考这个博客: 【CUDA 基础】5.6 线程束洗牌指令

cuSDDMM在多GPU上的可扩展性

CPU上的DRAM内存通常远远大于GPU上的全局内存容量. 用GPU进行加速计算的同时, 单个GPU的全局内存通常不足以容纳大型问题(如更大的矩阵), 这激发了对多GPU SDDMM解决方案的需求.

多GPU的利用主要为了解决单个GPU容量不足的问题. 多个GPU解决问题时, GPU之间需要进行数据通信和同步，存在一定的通信开销，特别是在数据量较大时可能会成为性能瓶颈.

根据上节提到SM-L2 方案. 将输入矩阵分为多个分块,每个块依次处理. 多节点方案中,可以在多台机器上并行启动内核, 从而可以同时处理多个块.

然而, 在不同节点上平均划分整个列可能会导致显著的负载不均衡. 例如一个稀疏矩阵中大多非零元素在左半边, 从中间平均划分导致其中一个节点计算量过大, 又由于"木桶效应", 计算瓶颈将会在出现在这个节点.

稀疏矩阵: 蓝色方块代表非零元素,白色方块代表0.

为了缓解这个问题, 采用了一种非对称的分区技术,根据稀疏矩阵S中每列非零的数量, 将S分成多个ID分块, 使每个分块都有相似的工作量. 其中稠密矩阵A或B的其中一个也被划分到不同的节点上, 另一个矩阵则被所有节点共享.

cuSDDMM性能测试

实验在 NAVIDIA Tesla P100 GPU机器上运行. 具有56 SMs, 64 cores/MP, 16 GB 全局内存, 1328MHz 时钟频率和4MB L2缓存.
CPU节点为 Intel(R) Xeon(R) CPU E5-2680 V4(28核).
图数据集来自SNAP和GraphChallenge.
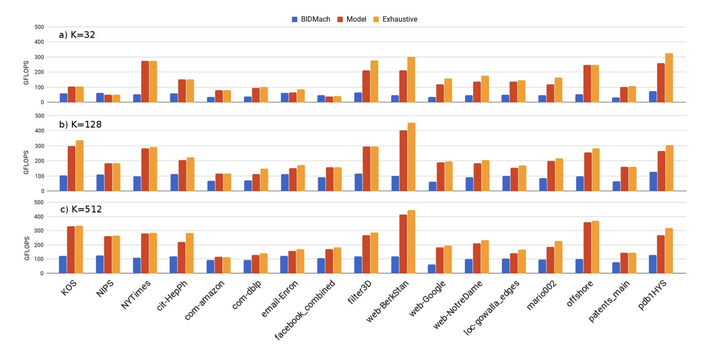
与BIDMesh库的SDDMM GPU实现进行比较. 加速效果最多达到4.6倍.

在Tesla P100 GPU上使用 a)K=32, b)K=128, c)K=512时的性能(GFLOPS), 蓝色代表BIDMach, 红色代表基于模型的cuSDDMM, 橙色代表使用cuSDDMM的穷举搜索.

结语

目前针对SDDMM内核中GPU不规则访问的问题的优化并不多.cuSPARSE库中缺乏优化的SDDMM函数是论文的动机. 对于SDDMM内核主要利用共享内存和L2缓存来合并全局内存访问.

可能有理解或表述不当的地方, 欢迎大家指正.

论文链接: Sampled Dense Matrix Multiplication for High-Performance Machine Learning