[论文笔记]用于稀疏矩阵乘法的自适应稀疏分块方法
<<Adaptive Sparse Tiling for Sparse Matrix Multiplication>>
论文于2019年发表在PPoPP '19: Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming.
分块(Tiling)是数据本地性优化的关键技术, 广泛应用于多核/众核CPU和GPU的高性能实现中. 然而, 稀疏矩阵乘法不规则和矩阵依赖的数据访问模式使得使用分块来增强数据重用变得困难. 在论文中, 设计了一种自适应分块策略, 并将其应用于两个基本操作:SpMM(稀疏矩阵-稠密矩阵乘法)和SDDMM( 采样稀疏矩阵-稠密矩阵乘法). 使用了标准的压缩稀疏行(CSR)格式, 并在其中进行行内重排以实现自适应分块. 使用来自Sparse Suite集合的大量矩阵进行实验评估, 表明与当前可用的最先进替代方案相比, 性能有了显著的提升.
文章链接: [论文笔记]用于稀疏矩阵乘法的自适应稀疏分块方法
Tiling
分块(Tiling)是有效利用数据重用的关键技术, 在所有高性能的密集线性代数计算, 卷积神经网络, 模板计算等的高性能实现中都有应用. 虽然对于此类规则计算的分块技术已经被充分理解和广泛应用, 并且在多核CPU和GPU上的高性能实现中得到了大量的使用,
但是将分块技术有效应用在稀疏矩阵乘法(SpMM)上却仍然存在挑战.
分块(Tiling)是将一个大的矩阵划分为多个小的子矩阵, 以便于在计算过程中充分利用数据重用性, 提高计算效率.
在稠密矩阵的分块中, 均匀分块是常见的做法, 其中所有分块(除了边界分块)具有相同数量的操作和相同的数据占用. 然而, 对于稀疏矩阵的分块, 由于稀疏矩阵在二维索引空间中非零元素的分布非常不均匀, 不同大小的分块中非零元素的数量会有明显的差异. 分块方法是否比非分块方法更能实现高性能取决于该区域的稀疏结构.
在论文中, 开发了一种自适应稀疏分块(ASpT)方法, 用于对SpMM(稀疏矩阵-稠密矩阵乘法)和SDDMM(采样稠密矩阵-稠密矩阵乘法)进行分块. 一个关键思想是, 二维块中每个"活跃"行/列段(至少包含一个非零元素)的平均非零元素数量 在决定二维块的分块执行或非分块执行的优劣方面起着重要作用. 稀疏矩阵被划分为行面板, 每个行面板中的活动列要么被分组为二维分块以进行分块执行, 要么由于其活动列密度不足而被分配到非分块执行.
SpMM和SDDMM
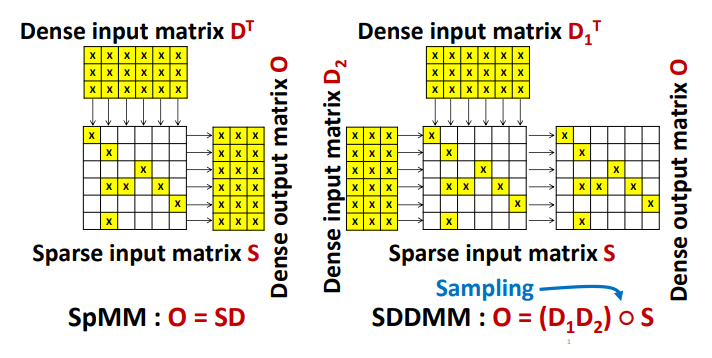
SpMM(稀疏矩阵-稠密矩阵乘法)是将稀疏矩阵$S$与稠密矩阵$D$相乘生成一个密集输出矩阵$O$的操作. 广泛应用于许多计算密集型领域, 包括求解矩阵特征值, 卷积神经网络(CNNs)和图计算等. 算法1展示了使用CSR表示的顺序SpMM运算.
SDDMM(采样稀疏矩阵-稠密矩阵乘法)是将两个稠密矩阵$D1$和$D2$相乘, 然后将结果矩阵与稀疏矩阵$S$进行元素级乘法(哈达玛积). 常用于机器学习中的稀疏模型计算, 例如 Gamma Poisson(GaP),稀疏因子分析(SFA)和交替最小二乘法(ALS). 算法2展示了使用CSR表示的顺序SDDMM运算.
哈达玛积(Hadamard Product)是两个矩阵的对应元素相乘, 得到的矩阵的每个元素是两个矩阵对应位置元素的乘积.
下图展示了SpMM和SDDMM的概念视图.
关于SpMM和SDDMM的更多介绍可以参考以往的笔记, 这里就简单概括一下.
数据重用的潜力
对于一个$N \times N$的带状稀疏矩阵, 假设带宽(带状矩阵的"带宽"是矩阵中心对角线左右两边包含非零元素的宽度)为$B$. 意味着每一行最多有$B$个非零元素. 总共$N$行, 因此矩阵的总非零元素约为$N \times B$. 与大小为$N \times K$的稠密矩阵进行矩阵乘法运算, 对于每个非零元素, 需要进行$K$次乘法和$K-1$次加法, 因此总的浮点运算次数约为$2 \times N \times B \times K$. 每个元素为单精度浮点数, 占用4字节.
带状矩阵: 矩阵中非零元素只分布在矩阵的对角线附近, 其他位置都是0. 带状矩阵的"带宽"
是指矩阵中心对角线左右两边非零元素的宽度(或者说个数).
带宽为1的4×4带状矩阵示例
- 对于稠密输入矩阵$D$和稠密输出矩阵$O$都是$N \times K$的矩阵.
- 所需的总储存需求为: $4 \cdot N \cdot K + 4 \cdot N \cdot K$ bytes
- 对于稀疏输入矩阵$S$ 总共有$N \cdot B$个非零元素. 在CSR储存表示中, 每个非零元素还有一个对应的列索引(数量为$N \cdot B$),
和行偏移数组(数量为$N + 1$).- 所需的总储存需求为: $4 \cdot N \cdot B + 4 \cdot N \cdot B + 4 \cdot (N + 1) \approx 4NB + 4NB + 4N$ bytes
矩阵运算所需的储存总需求可以表示为: $4NK + 4NK + 8NB + 4N$, 提取N为公因子再忽略影响较小的项, 可以得到近似表达式: $8N(K + B)$
数据重用的度量方式是操作强度(Operational Intensity), 即:
- $OI = \frac{浮点运算次数}{内存传输量(字节数)}$
数据重用的概念是, 如何在计算过程中尽量多次重复利用已经加载到缓存中的数据.
对于 $N \times K$的稠密矩阵和$N \times B$的稀疏矩阵, 浮点运算次数约为 $2NBK$, 而总内存传输量约为 $8N(K + B)$. 因此,
理论上的最大$OI$为:
- $OI_{max} = \frac{2NBK}{8N(K + B)} = \frac{BK}{4(K + B)}$ 倒数求和的形式: $\frac{1}{\frac{4}{B} + \frac{4}{4K}}$
因此, 随着带宽$B$的增加, $OI_{max}$会增加. 在实际测量的数据中显示, $OI$首先随着B的增加而增加, 然后由于L2缓存容量的限制而减少.
当算法1在遍历稀疏矩阵$S$的行时, 如果某一行的非零元素对应的列被多次访问之间的间隔过大(即在访问同一列之前, 访问了太多其他行的列数据), 则对应的稀疏矩阵$D$的列数可能会被从缓存中移除(cache eviction). 这会导致$D$的数据重用性显著降低,
因为数据需要频繁从主存中重新加载, 而不能充分利用缓存中的数据.
所以稀疏矩$S$的稀疏结构(非零元素的分布模式)直接决定了算法访问稠密矩阵$D$列的顺序和频率. 如果$S$的非零元素分布稀疏且不均匀, 则稠密矩阵$D$的列数据在缓冲中可能很快失效, 重用性下降. 如果$S$的非零元素集中在某些行或列, 则稠密矩阵$D$的重用性会显著提高.
三种数据访问方案对比
按行访问(Row-wise Access): 默认情况下, 使用CSR表示法如算法1中先按照行顺序(row-wise)访问稀疏矩阵$S$的非零元素. 这使得$D$的同一列的数据可能会跨多行被访问, 而不是集中在一次计算中访问, 导致$D$的列数据在缓存中的重用率低. 为了实现稠密矩阵$D$元素更好的重用, 必须改变稀疏矩阵$S$元素的访问顺序.
还有一种办法是按列访问(Column-wise Access): 完全按列访问$S$可以实现对$D$的列元素的最大化重用, 从而降低数据传输量,
但是可能会导致输出矩阵$O$的重用率下降. 因为$O$的每个元素需要在最内层循环中多次累加更新, 无法保持在缓存或寄存器中,
增加了缓存失效(cache miss)的可能性.
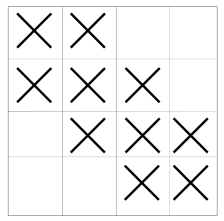
DCSC表示的列内按行访问(Column-wise Access within Row-panels): 通过将$S$分为多个行面板(row-panels), 然后在每个行面板中按照列的顺序访问. 使用双压缩稀疏列(DCSC)表示法, 将$S$的非零元素按照列分组压缩储存. 列内按行访问的模式可以让稠密矩阵$D$的列数据部分重用, 通过限制列访问的范围, 保持$O$的部分重用. 但是, DCSC的列访问模式导致单词操作设计的非零元素数量较小(列密度较小).
行面板(row-panels)是指针对稀疏矩阵$S$的行进行分块, 一个行面板是由稀$S$中连续的若干行组成的子块. 如果矩阵$S$
的大小是$M \times N$, 每个行面板包含$P$行, 那么$S$可以被分为$M/P$个行面板.
二维分块(2D Tiling): 将稀疏矩阵$S$划分为多个二维块(2D tiles), 然后对每个块的非零元素按照行顺序处理. 同时考虑了$D$ 和$O$的重用性. 每个二维块中, 稠密矩阵$D$的列数据和输出矩阵$O$的行数据可以在寄存器中重用. 但是, 二维分块的性能依赖于稀疏矩阵$S$的非零元素分布. 如果矩阵的非零元素非常稀疏, 某些二维块可能空置, 浪费计算资源.
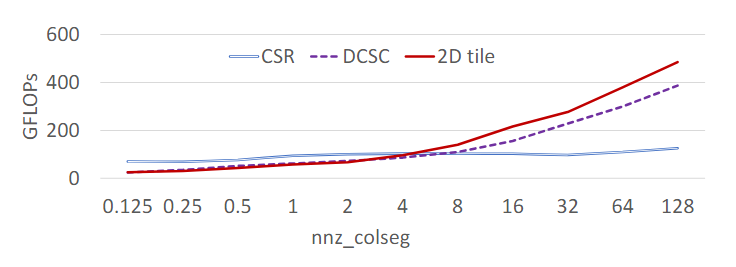
下图是基于随机生成的稀疏矩阵, 通过模拟不同的稀疏结构, 测试三种不同方法的性能.
三种方案的性能对比
- GFLOPS表示每秒十亿次的浮点运算数, 是一个衡量计算设备性能的指标. 数值越高表示性能越好
-
nnz_colseg表示平均每列段的的非零元素数量, 数值越高代表稀疏矩阵越密集, 数据重用潜力越大.
计算公式为: $\frac{TM \times nnz}{M \times N}$- $TM$: DCSC推荐的行段大小
- $nnz$: 稀疏矩阵的非零元素总数
- $M$, $N$: 稀疏矩阵的行数和列数
三种方法的优劣取决于稀疏矩阵的稀疏性(非零元素的分布模式). 每种方法适用于特定的矩阵结构, 无法单纯地依赖一种方法解决所有情况.
ASpT概述
本节概述了ASpT(自适应稀疏分块)方法, 这是一种使用无序压索稀疏行(CSR)表示法进行稀疏矩阵乘法分块的执行策略.
ASpT方案基于以下观察:
- 当nnz_colseg较高时, 二维分块的表现最佳, 因为它能充分利用列的高密度特性, 将数据重用率最大化
- 当nnz_colseg较低时, 标准的按行访问会更加高效, 因为稀疏性高的列段对分块的优化效果不明显
- **实验中, DCSC在任何场景下的性能都不会同时超过其他两种方法, 它在$D$元素的列数据重用的提升不足以弥补寄存器操作效率低的劣势
**
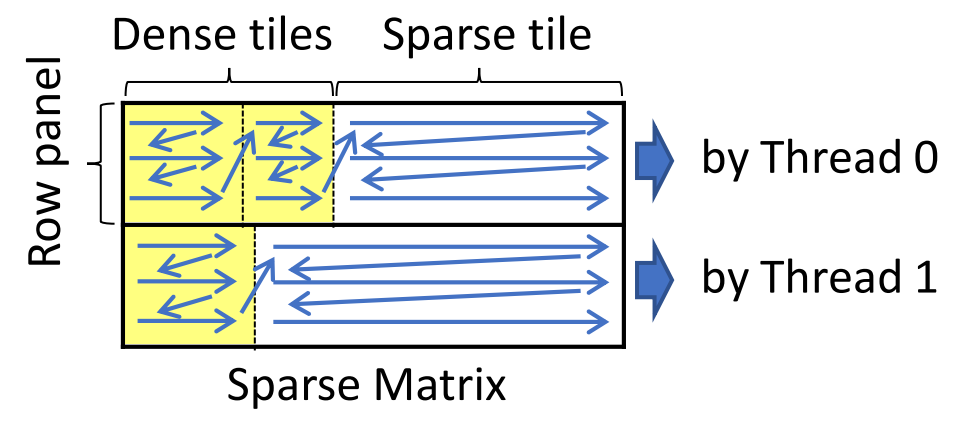
因此, ASpT选择CSR表示的按行访问(Row-wise Access)和二维分块(2D Tiling)方法的组合, 以适应不同的稀疏性. 根据稀疏矩阵不同区域的稠密程度动态选择策略. 下图展示了使用自适应稀疏分块(ASpT)方法背后的高级思想.
在多个内核上使用ASpT进行稀疏矩阵乘法
ASpT方法首先将稀疏矩阵$S$划分为多个行面板(row-panels), 行面板的大小(行数)由缓存(L2 cache)或内存容量限制来决定. 然后对每个行面板通过阈值(阈值通过上节中的测试确定, 是 CSR 和 2D Tile 性能的交叉点)分为高密度的稠密块(Dense tiles) 和低密度的稀疏块(Sparse tile). 高密度列段使用 2D tiling 方法处理, 低密度列段直接采用 row-wise CSR 方法. 为了实现这一优化, ASpT 会对每个行块内的列段进行重新排序, 使高密度列段优先处理并划分为 2D tiles, 而低密度列段被集中放置, 用于未分块的CSR计算.
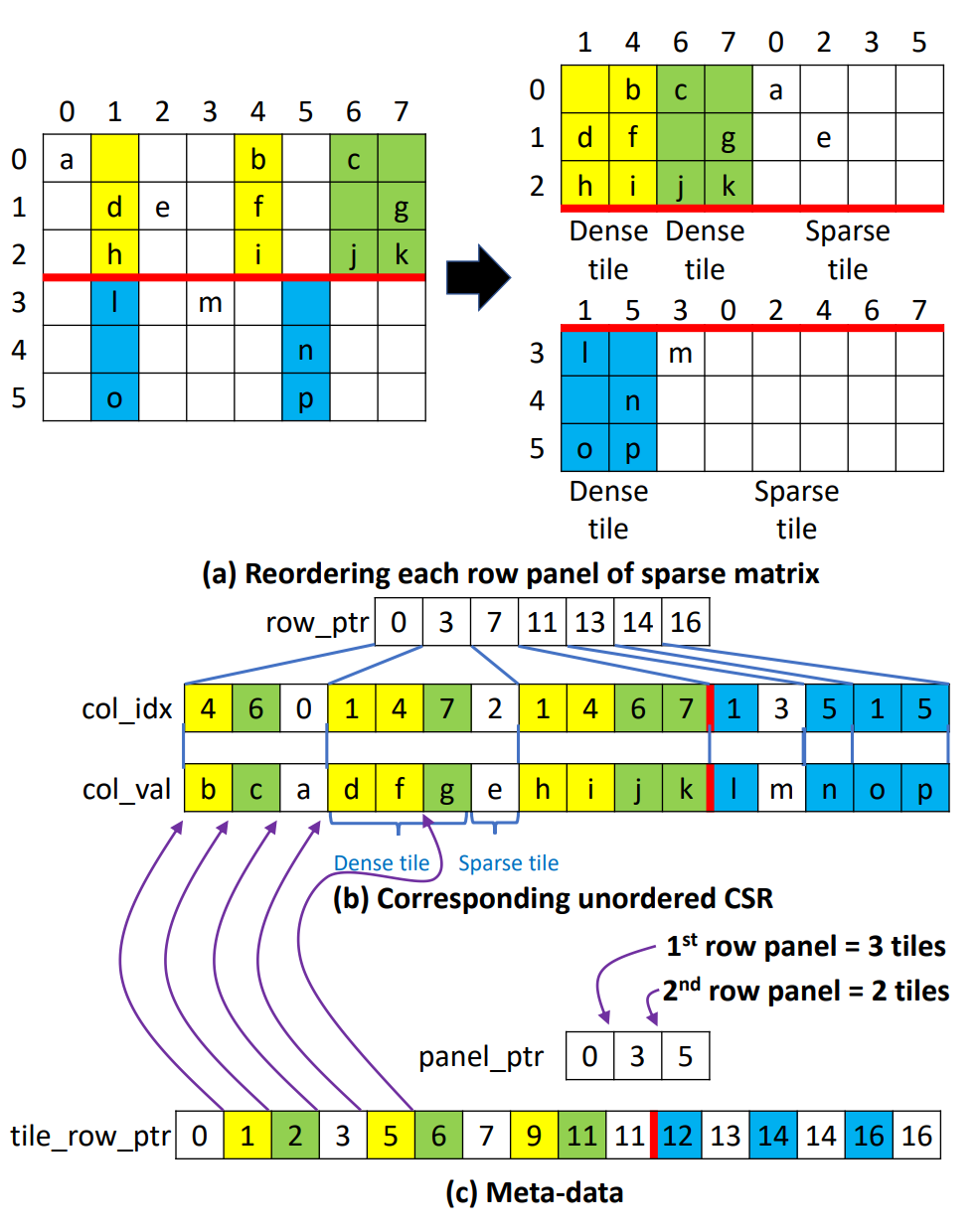
数据表示
SpMM方案使用带有额外元数据的无序CSR表示, 如下图所示, (a)和(b)分别展示了稀疏矩阵的概念视图和相应的无序CSR表示. 在(a)中, 整个矩阵被划分为两个行面板, 每个行面板包含一组连续的行. 如果行面板中的列段包含至少两个非零元素, 则被归类为高密度列段. 稀疏矩阵的每个行面板按照图(b)所示的方式重新排序. 行面板中的所有高密度列段都放置在低密度列段之前.
将稀疏矩阵拆分为高度聚类的行段和剩余部分
因此, 每个重新排序的行面板可以看成两个部分: 第一个部分包含一组高密度列段, 第二个部分由低密度列段组成. 并且第一个部分进一步细分为 2D tiles, 而整个第二个部分视为单个2D tile. 行面板中的第一个部分的2D tiles的宽度选择适合于缓存(或共享内存)的大小.
GPU共享内存和寄存器的利用
在传统多核CPU或多线程架构中, L1/L2缓存通常只有少量线程同时访问. 这种设计适合密集计算任务, 并且缓存压力较小. 每个线程可以分到较多的缓存空间, 缓存冲突较少. 而GPU的特点是并行度极高, 可能有成千上万个线程同时运行, 例如NVIDIA Pascal P100 GPU支持多达2K线程访问24KB的L1缓存, 以及112K线程访问4MB的L2缓存. 大量线程同时访问缓存会导致单个线程可用的缓存空间显著减少. 如果每个线程访问唯一的内存位置, 那么每个线程仅能使用$\frac{24KB}{2K} = 12B/threads$ 的L1缓存和$\frac{4MB}{112K} = 37B/threads$的L2缓存.
然而, GPU的每个流式多处理器(SM)都有大量的寄存器和共享内存. 例如P100美格SM的寄存器储存容量为256KB, 共享内存容量为64KB. 并且P100的共享内存带宽高于一级缓存. 相较于缓存, 寄存器和共享内存是GPU内存优化的重点.
寄存器优化的前提是只有访问模式可以静态确定的数据, 才能分配到寄存器中, 动态或不规则的访问模式无法利用寄存器. 在稀疏矩阵乘法中, 输出稠密矩阵$O$的元素是按行逐一计算, 访问模式是顺序且可预测的, 这些元素可以放置在寄存器中储存. 输入稠密矩阵$D$的访问取决于稀疏矩阵$S$的稀疏结构, 因此, 这些访问保存在共享内存中.
SpMM的ASpT实现
列表2和列表3分别展示了针对密集块和稀疏块的SpMM-ASpT的GPU实现.
线程分布与映射:
- 每个线程块处理一个2D tile
- 在线程块内部, 不同的线程束(warp)处理行块中的不同行,
线程束内的线程沿着K方向分布, 以避免线程发散, 并实现良好的负载均衡
针对密集块和稀疏块的SpMM-ASpT的GPU实现
对于稠密2D tiles会将$D$的相应元素加载到共享内存中, 以便多次重用提高访问效率. 对于稀疏2D tiles, 因为非零元素较少, 直接从全局内存中读取访问.
算法首先初始化行块和索引, 包括行块ID(row panel id), 行偏移量(row offset)以及线程组内索引(slice index), 以便线程定位需要处理的数据. 对于稠密块, 所有线程协作将$D$的对应部分加载到共享内存中, 同时利用 map_id 跟踪原始列索引, 确保正确访问数据.
在计算阶段, 每个 warp 并行处理不同的行, warp内线程沿$K$维分布, 以避免线程发散, 并实现良好的负载均衡. 计算结果先存储在寄存器中, 减少中间存储的内存写入, 行块计算完成后再统一写回全局内存.
SpMM-ASpT GPU 算法通过动态选择稠密和稀疏 tile 的处理方式, 结合共享内存和寄存器优化, 显著提升了稀疏矩阵乘法的性能, 同时确保了线程的高效并行与硬件资源的充分利用.
SDDMM的ASpT实现
在SDDMM中, 两个稠密矩阵相乘, 然后将结果矩阵使用元素级乘法(哈达玛积)与一个稀疏矩阵进行缩放. 下图展示了针对密集块和稀疏块的SDDMM-ASpT的GPU实现.
针对密集块和稀疏块的SDDMM-ASpT的GPU实现
在GPU实现上, 算法动态选择稠密块和稀疏块的处理方式. 对于稠密块, 密集矩阵$D1$加载到共享内存中. 对于稀疏块, $D1$ 的数据直接从全局内存中访问. 稠密矩阵$D2$的元素无论稠密块还是稀疏块都储存在寄存器中. 计算得到的输出矩阵$O$ 的中间结果保存在线程私有的寄存器中, 使用线程束的shffle进行归约. 累积的输出值经过缩放后写入全局内存.
实验评估
- 实验设备:NVIDIA P100 GPU(56个 Pascal SMs, 16GB全局内存, 带宽为732GB/s, 4MB L2缓存, 每个SM有64KB共享内存)
- 数据集: 来自SuiteSparse集合的975个矩阵, 矩阵覆盖了至少10000行, 10000列和100000个非零元素
- 使用单精度(SP)和双精度(DP)计算, 测试稠密矩阵宽度(K)为32和128的不同配置, 仅包含核心计算时间, 不计入预处理或数据传输时间
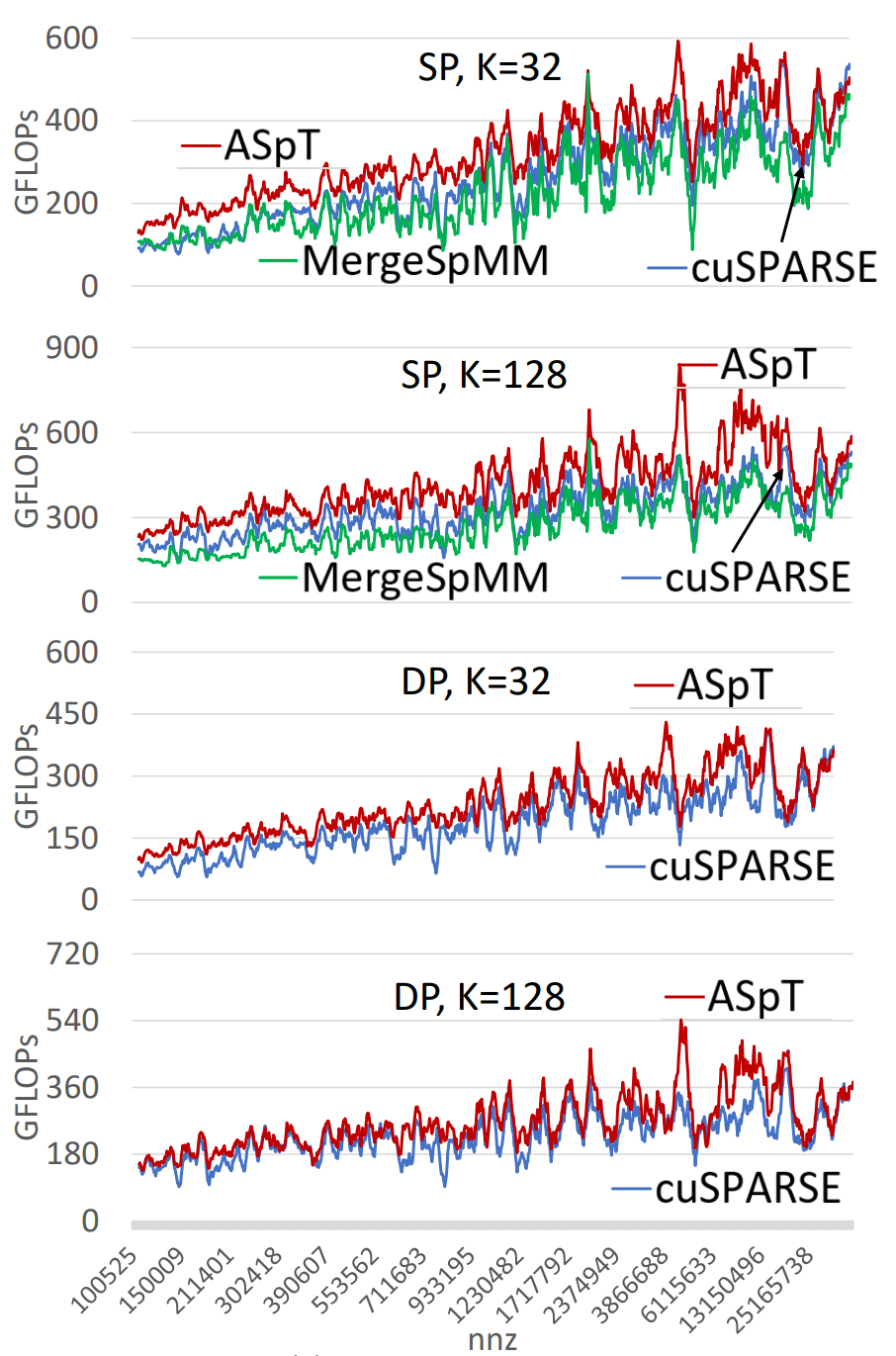
- 在SpMM测试中, 与NVIDIA cuSPARSE库的性能进行比较
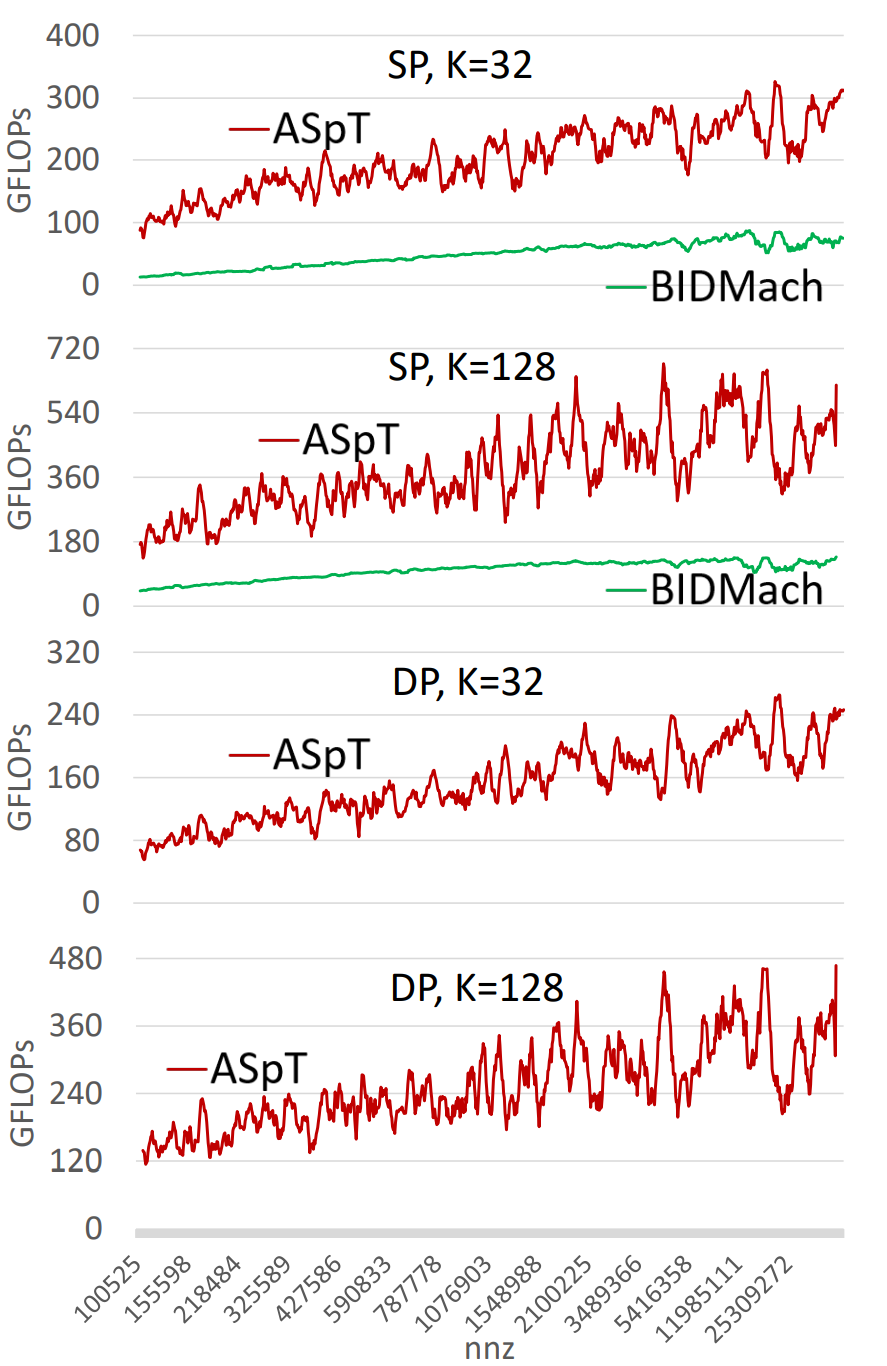
- 在SDDMM测试中, 与BIDMach库的性能进行比较
P100的SpMM结果
结果显示, ASpT显著优于cuSPARSE, 在高宽度稠密矩阵(K=128)情况下表现尤为突出. 对于特定数据集, ASpT的性能可达到900 GFLOPs, 而cuSPARSE的最高性能约为685 GFLOPs. ASpT在稠密宽度较大的场景中, 性能提升显著, 显示了对大规模矩阵运算的适应性.
P100的SDDMM结果
结果显示, ASpT显著优于BIDMach，在所有测试矩阵上表现优异. 随着稠密矩阵宽度(K)增加, ASpT性能进一步提升. 说明其GPU优化策略的适用性.
在不同平台和任务下, ASpT均展现了显著的性能提升, 尤其在稠密矩阵宽度较大和稀疏矩阵规模较大的场景中.
结语
SpMM和SDDMM是许多机器学习应用中的关键核心. 与其他使用定制化的稀疏矩阵表示(例如DCSC等)来实现高性能的努力不同, 论文的目标是利用标准(无序)CSR稀疏矩阵表示来高效地实现这些基本操作. 设计了一种自适应二维分块方法, 展现了更高的内存重用潜力. 与当前最先进的技术相比, ASpT-SpMM在GPU上实现了高达24.21倍的加速, 几何平均值为1.35倍, ASpT-SDDMM在GPU上实现了最多13.74倍的加速, 几何平均值为3.60倍.
论文中还描述了在多核CPU中的实现方法, 并且实验显示优于现有的最先进的代替方法(Intel MKL库, TACO). 由于本人只专注于GPU实现, 所以没有过多关注, 详细内容在论文主体部分有详尽阐述.
可能有理解或表述不当的地方, 欢迎大家指正.
论文链接: Adaptive Sparse Matrix-Matrix Multiplication on GPUs
开源链接: ASpT-mirror